前面的章节中讨论轴向拉伸(压缩)杆件的强度计算时,我们知道只要拉、压杆截面上的正应力不超过材料的许用应力,杆件就满足强度要求。但是,对于工程中较细长的压杆除了应该考虑其强度问题以外,还需要考虑其平衡的稳定性问题。例如,有一根钢锯条,横截面尺寸为10mm×1mm,钢的许用应力取[σ]=300MPa,按照强度条件计算可得钢锯条所能承受的轴向压力

F=[σ]A=(300×10×1)N=3000N=3kN

但是,当我们将此钢锯条竖放在桌上,用手压其上端,会发现压力不到30N时,锯条就被明显压弯。显然,30N比3kN小很多,而且当钢锯条被明显压弯时,就不能再承担更大的压力。由此可见,钢锯条的承载能力并不取决于轴向压缩的抗压强度,而取决于钢锯条受压时能否保持直线形态的平衡。

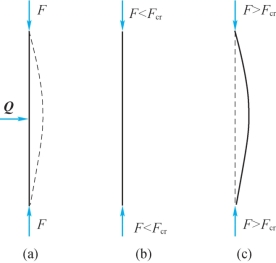
为了方便对压杆的承载能力进行理论研究,通常将压杆假设为由均质材料制成、轴线为直线且外加压力的作用线与压杆轴线重合的理想中心受压直杆力学模型。下面利用这一模型说明压杆稳定性的概念。图13-1(a)所示中心受压直杆承受轴向压力F作用后,给杆施加一微小的横向干扰力Q,使杆发生弯曲变形,然后撤去横向力Q。试验表明,当轴向压力不大时,撤去横向力后,杆的轴线将恢复其原来的直线平衡形态,如图13-1(b)所示,那么压杆原来直线形态的平衡是稳定的;当轴向力增大到一定的临界值时,撤去横向力Q后,杆的轴线将保持弯曲的平衡形态,而不再恢复其原有的直线平衡形态,如图13-1(c)所示,那么压杆原来直线形态的平衡是不稳定的。从上述现象中,我们可以发现压杆原直线形态的平衡是否稳定,和压杆承受的轴向压力F有关。中心受压直杆直线形态的平衡,由稳定平衡转化为不稳定平衡时所受轴向压力的临界值,称为临界压力或简称临界力,用Fcr表示。受压直杆在临界压力(抑或大于临界压力的压力)作用下丧失稳定性,简称为失稳。研究压杆稳定性问题的关键是确定其临界压力。若压杆的工作压力不超过临界压力,则压杆不致失稳。

(www.daowen.com)

图13-1

需要注意的是,实际中的压杆轴线难免有初曲率、外力合力作用线与压杆轴线并非完全重合以及材料并非绝对均匀,这些因素都可使压杆受压力作用时发生弯曲变形。实际压杆的平衡稳定性问题是在压力作用下,杆的弯曲变形是否会出现急剧增大而丧失正常的承载能力。

思政提示

构件丧失稳定性往往会突然发生而且有较大的危害性,保证和维护好其稳定性就相当重要。同样地,我们也需要构建、维护好一个和谐稳定的社会。和谐与稳定符合国家和人民的根本利益,促进和谐与维护稳定是我们每一个公民的责任和义务。