在第7章中,研究杆件的扭转时只考虑了扭矩对杆的作用。实际上,工程中的许多受扭杆件,在发生扭转变形的同时,通常还会发生弯曲变形,当这种弯曲变形不能忽略时,则应按弯曲与扭转的组合变形问题来处理。例如,图12-5所示的传动轴,在两个轮子的边缘上作用有沿切线方向的力P1和P2,这些力不但会使轴发生扭转,同时还会使轴发生弯曲。本节将以圆截面杆为研究对象,介绍杆件在扭转与弯曲组合变形情况下的强度计算问题。

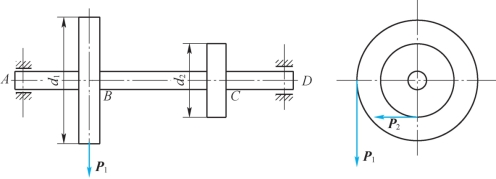
图12-5

图12-6(a)所示机轴,其横截面为直径d的圆形。在轴的左端有一重为W、半径为R的皮带轮,轴转动时,皮带中的拉力分别为T和t(T＞t),轴的右端为一曲柄,曲柄把手上的力P总是垂直于曲柄平面。

(1)内力分析。

为了求得在机轴各个截面上的扭矩Mn、弯矩M和剪力Q,将各个外力对轴心进行简化。

现在研究图12-6(a)中3个力P、T、t与水平轴Oz平行时的情形。为了计算机轴的内力,将左端作用在轮周的拉力T与t对点O进行简化,得到作用在杆轴上的水平力(T+t)和扭转外力偶矩(T-t)R。同样,将右端作用在手柄上的力P向机轴延长线上的点E进行简化,得到水平力P与扭转外力偶矩Ph,如图12-6(b)所示。容易看出,扭转外力偶矩将使机轴发生扭转,水平力和竖直力将使机轴发生弯曲。当机轴处在等速转动的平衡状态时,机轴受到的扭矩为

Mn=(T-t)R=Ph

机轴的扭矩图如图12-6(c)所示。

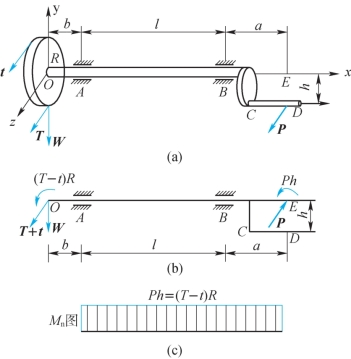
图12-6

当力(T+t)、P、W使机轴弯曲时,支承A与B可以看作铰支座。这样,竖直力W使机轴在竖直平面内引起的弯矩图如图12-7(a)所示,水平力(T+t)和P使机轴在水平面内引起的弯矩图如图12-7(b)所示。在机轴每个截面上的总弯矩应等于在竖直方向的弯矩和在水平方向的弯矩的几何叠加。例如,在机轴的截面A上的总弯矩为

一般各个截面在竖直方向和水平方向的弯矩都互不相同,而对于圆形截面轴,截面上的任一直径都是形心主轴,截面对任一直径的抗弯截面模量都相等,故可将各个截面上的总弯矩都画在同一平面内,得到如图12-7(c)所示的总弯矩图。由总弯矩图可以看出,机轴中的最大弯矩发生在截面A或B上。

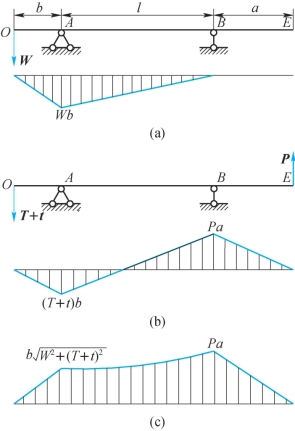
图12-7

(2)应力分析。

由于扭矩Mn的作用,在圆截面上产生切应力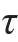=Mnρ/Ip,它在圆截面的边缘(　ρ=d/2)达到最大值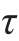n=Mn/Wp,方向与圆截面的周边相切,如图12-8(a)所示。对于实心圆轴,其抗扭截面模量Wp=πd3/16。

弯矩M作用在水平面上,使圆形截面水平直径的两端点处产生最大正应力σM=M/W,如图12-8(b)所示。对实心圆轴来说,其抗弯截面模量W=πd3/32,且Wp=2W。

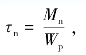由上面的分析可知,应力的最不利组合情况肯定会发生在最大弯矩和最大扭矩所作用的横截面的边缘处。故为了进行强度计算,分析图12-8(c)中的某些边缘点(如点1)的应力状态。在图12-8(d)中表示了由点1取出的单元体。在单元体1上,将有由弯矩M产生的正应力σM=与由扭矩Mn产生的切应力弯扭组合变形危险点处的3个主应力分别为

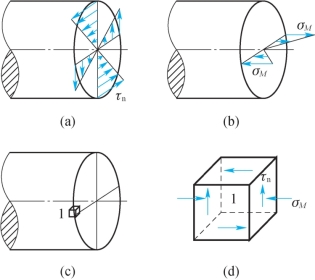
图12-8

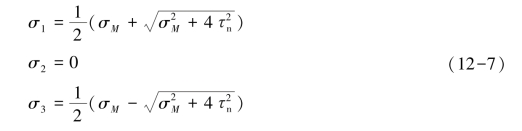
(3)强度计算。

承受弯、扭的圆轴一般都是由延性金属材料制成的,故可按第三或第四强度理论建立强度条件。

第三强度理论,计算相当应力:σr3=σ1-σ3=

第四强度理论,计算相当应力:σr4=

强度条件:σr≤[σ]。

特别地,对于圆截面杆,Wp=2W,强度条件还可以写为

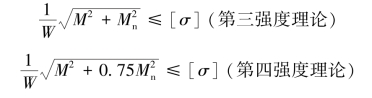
式中,M为危险截面上的弯矩,Mn为危险截面上的扭矩。

例12-3　试根据最大切应力理论(第三强度理论)确定图12-9所示手摇卷扬机(辘轳)能起吊的最大许可载荷P。已知:机轴的横截面为直径d=30mm的圆形,机轴材料的许用应力[σ]=160MPa。

图12-9

解:在力P作用下,机轴将同时发生扭转和弯曲变形,应按扭转与弯曲组合变形问题计算。

(1)跨中截面的内力。

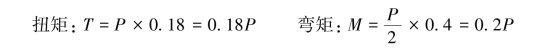
(2)截面的几何特性。

(3)应力计算。

根据第三强度理论,强度条件为

即

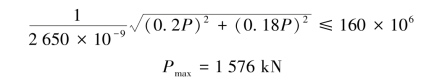
例12-4　如图12-10(a)所示传动轴,传递功率P=7.5kW,轴的转速n=100r/min,A、B为皮带轮,轮A上的皮带为水平,轮B上的皮带为铅直,若两轮的直径为600mm,则已知F1＞F2,F2=1500N,轴材料的许用应力　σ[]=80MPa,试按第三强度理论计算轴的直径。

解:

(1)外力计算。

作用在轮A与轮B上的扭力偶矩为

将皮带张力F1与F2向轴AB轴线简化,由平衡方程得

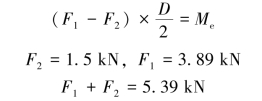
如图12-10(b)所示。

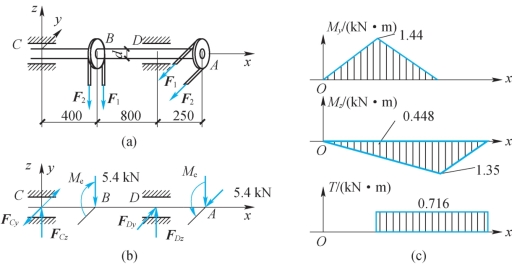
图12-10

(2)内力分析。

扭力偶矩Me使轴扭转;轮B上铅直方向载荷F1与F2使轴在铅垂面(即xz平面)内弯曲;轮A上水平方向载荷F1与F2使轴在水平面(即xy平面)内弯曲。轴的弯矩My、Mz与扭矩T如图12-10(c)所示。

对于圆形截面,任一直径均为截面的对称轴。因此,如果求得横截面上的总弯矩(www.daowen.com)

则横截面上的最大弯曲正应力

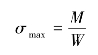
(3)截面设计。

显然,截面B为危险截面,该截面的总弯矩与扭矩分别为

于是,根据第三强度理论,危险点处的相当应力需要满足

即

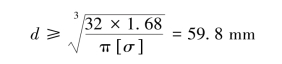
本章在讨论了应力状态、强度理论之后,着重讨论了组合变形分析。需要指出的是:在线弹性、小变形条件下,研究组合变形的方法是叠加法。将组合变形分解成几种基本变形,分别计算各种基本变形下的内力、应力、应变或位移,然后将同一处的结果相叠加,即可得到构件在组合变形情况下的内力、应力、应变和位移。本章虽然只研究了组合变形的应力分析和强度计算,但应当知道,只要是线弹性、小变形的情况,利用叠加法同样可以研究复杂组合变形结构和构件的变形和位移。

思政提示

组合变形问题是一类复杂且综合性强的问题,同时也是在实际工程中我们会经常面对的一类问题。从本章的介绍中可以看出,组合变形问题的分析求解过程烦琐复杂,且涉及的知识点较多。实际上我们在今后的科学研究或工作中,也会遇到很多复杂的问题,会面对诸多困难。不过正所谓“科学有险阻,苦战能过关”,一个合格的工程师必须要有不畏艰难、勇往直前的精神。

习　题

12-1　题12-1图所示为一木悬臂梁,梁长l=2m,矩形截面b×h=0.15m×0.3m,集中载荷P=800N,要求:

(1)计算α为0°和90°时的最大拉应力,并指出最大拉应力发生在什么地方;

(2)计算α为45°时的最大拉应力,并指出最大拉应力发生在什么地方。

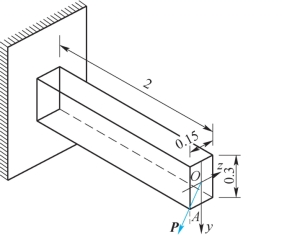
题12-1图

12-2　试证明对于矩形截面梁,当集中载荷P沿矩形截面的一对角线作用时,其中性轴将与另一对角线重合。

12-3　题12-3图为一搁置在屋架上的檩条的计算简图。已知:檩条的跨度l=5m,均布载荷q=2kN/m,矩形截面b×h=0.15m×0.20m,所用松木的弹性模量E=10GPa,许用应力[σ]=10MPa,檩条的许用挠度为[w]=,试校核檩条的强度和刚度。

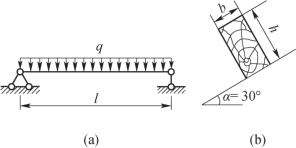
题12-3图

12-4　题12-4图所示为一简支梁,选用了25a工字钢。已知:作用在跨中的集中载荷P=5kN,载荷P的作用线与截面的竖直主轴间的夹角α=30°,钢材的弹性模量E=210GPa,许用应力[σ]=160MPa,梁的许用挠度[w]=图中长度单位为m。试对此梁进行强度校核和刚度校核。

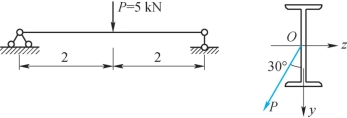
题12-4图

12-5　题12-5图所示为一浆砌块石挡土墙,墙高4m。已知:墙背承受的土压力pa=137kN,　且其作用线与竖直线之间的夹角α=45.7°,浆砌块石的密度ρ1=2.345×103kg/m3,墙基混凝土的密度ρ2=2.396×103kg/m3,其他尺寸如图所示。试取1m长的墙作为计算对象,求墙A、B、C、D各点处的正应力。

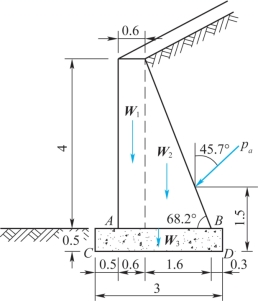
题12-5图

12-6　题12-6图所示为一渡槽的空心墩。已知:墩上承受的水重W3=2400kN,渡槽槽身重W2=2143kN,在截面AB以上部分墩身的自重W1=5115kN,风压力对截面A—B上y-y轴产生的力矩My=7514kN·m,截面A—B的面积S=4.67m2,抗弯截面模量Wz=6.42m3。试求作用在截面A—B以上的最大正应力和最小正应力。

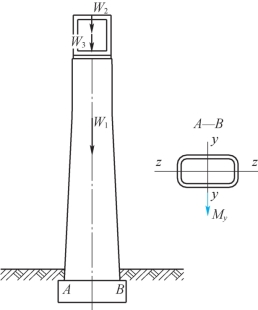
题12-6图

12-7　题12-7图所示为某渡槽刚架的基础。已知:在它的顶面受到由柱子传来的弯矩M=110kN·m、轴力N1=980kN和水平剪力Q=60kN,基础的自重和基础上土重的总重为N2=173kN,图中长度单位为m。试作出在基础底面的反力分布图(假定反力是按直线规律分布的)。

12-8　题12-8图所示为的混凝土重力坝,剖面为三角形,坝高h=30m,混凝土的密度为2.396×103kg/m3。若只考虑上游水压力和坝体自重的作用,在坝底截面上不允许出现拉应力,试求所需的坝底宽度B和在坝底上产生的最大压应力。

题12-7图

题12-8图

12-9　题12-9图为链条中的一环,受到拉力P=10kN的作用。已知链环的横截面为直径d=50mm的圆形,材料的许用应力[σ]=80MPa。试校核链条的强度。

12-10　受拉构件形状如题12-10图所示,已知截面尺寸为40mm×5mm,通过轴线的拉力P=12kN。现拉杆开有切口,如不计应力集中影响,当材料的[σ]=100MPa时。试确定切口的最大许可深度,并绘出切口截面的应力变化图。

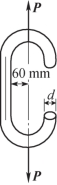
题12-9图

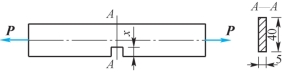
题12-10图

12-11　一圆截面直杆受偏心拉力作用,偏心距e=20mm,杆的直径为70mm,许用拉应力[σ]为120MPa,试求此杆的许可偏心拉力值。

12-12　求题12-12图中所示杆内的最大正应力(力P与杆的轴线平行)。

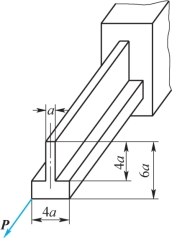
题12-12图

12-13　试画出题12-13图所示截面的截面形心,图中长度单位为mm。

题12-13图

12-14　题12-14图为一标志牌,支在外直径为50mm、内直径为40mm、高为3000mm的圆管上。若标志牌的尺寸为1000mm×1000mm,作用在标志牌上风压力的压强为400Pa,试求由于风压作用使管底截面在点A处产生的主应力和点B、C处产生的切应力。

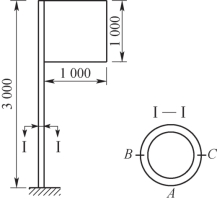
题12-14图

12-15　如题12-15图所示,直径为600mm,重量为2kN的皮带轮,随着横截面直径为50mm的圆轴一同转动。已知皮带中的拉力为8kN和1.5kN,轴承与皮带轮间的距离为150mm,试计算圆轴在轴承处的主拉应力和最大切应力。设圆轴材料的许用应力[σ]=160MPa,试按第三强度理论(最大切应力理论)进行强度校核。

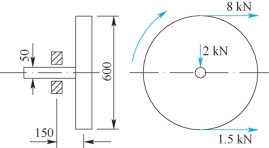
题12-15图