构件承受拉伸(或压缩)与弯曲组合变形的最一般情况如图12-2所示。构件在轴力FN的作用下发生沿x轴方向的拉伸变形;在弯矩Mz的作用下发生xy平面内的弯曲;在弯矩My的作用下发生xz平面内的弯曲变形。

在轴力FN的作用下,截面各处的拉伸正应力

在弯矩Mz的作用下,截面各处的弯曲正应力

在弯矩My的作用下,截面各处的弯曲正应力

图12-2

应当指出的是:必须注意截面各处弯曲正应力的符号。在图12-2所示坐标系和内力情况下,弯矩Mz作用时,坐标y为正的一侧受拉;弯矩My作用时,坐标z为正的一侧受拉。

由叠加法可得到截面上任意一点(y,z)的正应力

对于矩形截面,在图12-2中角点A处,y=ymax＞0,z=zmax＞0,拉应力最大,有

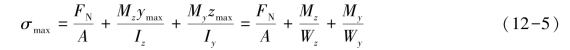
在图12-2中角点B处,y=ymax,z=zmax,拉应力最小(或者说压应力最大),有

式中,Iz、Wz,Iy、Wy分别是截面对z、y轴的惯性矩和抗弯截面模量。求得危险点应力后,即可选择适当的强度理论校核其强度。

例12-1　立柱如图12-3所示,在点A处受力F作用,点A在截面上的坐标为(y,z),求柱中的最大应力。

图12-3

解:将力F平移至截面形心C处,可知立柱受力F作用发生纵向压缩;受力偶矩My=Fz作用在xz平面内发生弯曲;受力偶矩Mz=Fy作用在xy平面内发生弯曲。(www.daowen.com)

柱中的最大压应力

柱中的最大拉应力

例12-2　如图12-4(a)所示,矩形截面梁AB高h=60mm,宽b=40mm,已知[σ]=120MPa,试校核其强度。

图12-4

解:(1)求约束力。

根据图12-4(a)所示整体受力图,列平衡方程

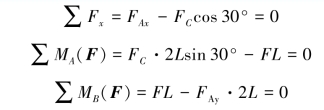
解得

(2)画内力图

梁AB内力图如图12-4(b)所示。

(3)危险点应力计算。

梁AB在L=500mm处弯矩最大,是危险截面,M为正,梁上缘受压,下缘受拉;截面各处在轴力作用下还受到压缩。叠加后梁上缘压应力值最大,且有

梁强度足够。

思政提示

危险点作为构件中“最弱”的位置决定了构件的成败,就好比最短的木板决定了木桶的盛水量。其实我们每个人也有着自身的“危险点”,我们应该多多思考一下自己的“短板”所在,并尽早补足,从而提高自己的综合素质。