形状改变比能理论认为形状改变比能(畸变能)密度是引起屈服的主要因素,畸变能的极限值通过单向拉伸试验求得。材料在单向拉伸下屈服时正应力为σs,相应的畸变能密度为在任意应力状态下,只要畸变能密度σd达到,便引起材料的屈服。故得屈服准则为σd≤

在任意应力状态下有

整理后把σs除以安全因数得许用应力　σ[],于是这一理论的强度条件为

试验表明,该理论对于塑性材料如钢、铜、铝的薄管试验结果能较好吻合,且比第三强度理论更能符合试验结果。

把4个强度理论的强度条件写成以下统一形式

式中,　σ[]为材料的许用应力;σr为复杂应力状态下按不同强度理论,由3个主应力按一定形式组合而成的应力值,称为相当应力。从第一强度理论到第四强度理论的顺序,相当应力分别为

这些强度理论均仅适用于常温、静载条件下的均质、连续、各向同性的材料。一般情况下,铸铁、石料、混凝土、玻璃等脆性材料,破坏时通常表现为断裂的形式,故宜采用第一强度理论和第二强度理论;碳钢、铜、铝等塑性材料,破坏时通常表现为屈服的形式,故宜采用第三强度理论和第四强度理论。

即使是同一材料,其破坏形式也会随应力状态的不同而不同。例如,低碳钢材料的试件在单向拉伸下以屈服的形式失效,但在三向拉伸应力状态下,且3个主应力值接近时,发生脆性断裂。又如,铸铁单向受拉时以断裂的形式失效,但将淬火后的钢球压在铸铁板上,接触点附近的材料处于三向受压状态,随着压力的增大,铸铁板会出现明显的凹坑,引起塑性变形。以上例子说明材料的失效形式是与应力状态有关的。无论是塑性还是脆性材料,在三向拉应力相近的情况下,都以断裂的形式失效,宜采用第一强度理论或第二强度理论;在三向压应力相近的情况下,都可以引起塑性变形,宜采用第三强度理论或第四强度理论。

例11-7　如图11-10所示,由Q235钢制成的两端封闭的圆柱形薄壁容器,外径D=1m,壁厚δ=10mm,容器内承受蒸汽内压p=3MPa,Q235钢的许用应力为　σ[]=160MPa,试校核该容器壁的强度。

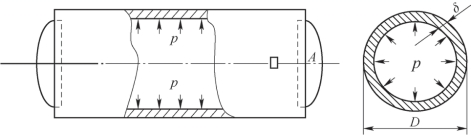
图11-10

解:(1)圆筒轴向横截面上的正应力σ′为

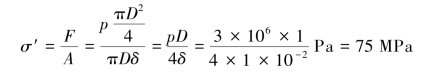
(2)求圆筒径向纵截面上的应力σ″。

由圆筒及其受力的对称性可知,所有过圆筒轴线的径向纵截面都是对称面,其上切应力为0,只有正应力σ″。由于圆筒壁厚远小于直径,可认为正应力σ″沿壁厚均匀分布。现从圆筒中取出一端相距l的圆环,并沿直径方向截开,取其上部分,由平衡条件得

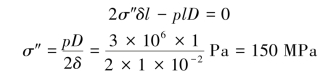
在圆筒壁上任一点A周围截取单元体,忽略内壁的压强p作用,于是得到双向应力状态,并且σ″和σ′皆为主应力,则有

(3)强度校核。

用第三强度理论进行校核:σr3=σ1-σ3=(150-0)=150MPa＜　σ[]。

所以,满足第三强度理论的强度条件。

用第四强度理论进行强度校核

所以,薄壁圆筒也满足第四强度理论的强度条件。

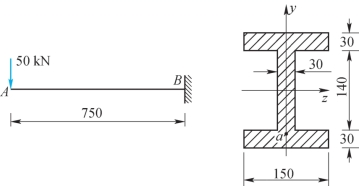
例11-8　一工字形截面简支梁受力如图11-11(a)所示,工字形截面尺寸由图11-11(b)给出,已知钢的许用应　[σ]=170MPa,[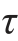]=100MPa,图中长度单位为mm。试全面校核该梁的强度。

图11-11

解:

(1)作梁的剪力图和弯矩图(图略)。在截面C、D处弯矩和剪力最大。所以C、D是危险截面,其弯矩和剪力分别为Mmax=100kN·m,FQmax=100kN。

(2)校核弯曲正应力强度。

先计算横截面对中性轴z轴的惯性矩:Iz=11075.5×10-8m4。

最大正应力发生在截面C、D的上下边缘各点,其值为

满足正应力强度条件。

(3)校核切应力强度。

计算横截面上中性轴以下面积对中性轴z轴的静矩:

危险截面上中性轴上的最大切应力: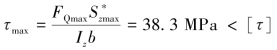=100MPa。

满足切应力强度条件。

(4)校核主应力。

在危险截面C和D,距中性轴最远的上下边缘处有最大正应力,在中性轴上有最大切应力,通过上面的计算可知这两处的强度是满足要求的。但是在截面C、D上内力M、FQ具有最大值。而且在截面腹板和翼缘交接处正应力和切应力都相当大,故该点的主应力也就较大,有可能是造成梁破坏的危险点,所以有必要选择适当的强度理论对截面腹板和翼缘交接处各点进行主应力校核。为此,考虑图11-11(b)所示的点a,围绕点a沿横截面和水平截面截出一个单元体,其横截面上的正应力和切应力分别为

其中,是截面的下翼缘面积对中性轴的静矩,且

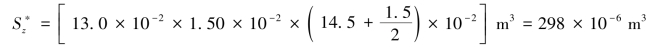
点a处于双向应力状态,则

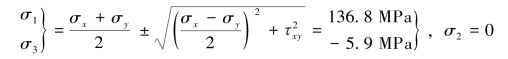
因为该工字钢是塑性材料,所以采用第三强度理论进行校核

采用第四强度理论进行校核

满足强度条件,所以该梁是安全的。

思政提示

在对构件进行强度校核时,通常对于脆性材料宜采用第一强度理论和第二强度理论,对于塑性材料宜采用第三强度理论和第四强度理论。在学习和工作中,我们在做事、想问题时,要根据事情的不同情况采取不同措施,不能一概而论。只有具体问题具体分析,才能找出解决问题的正确方法。

习　题

11-1　单元体如题11-1图所示。试求:(1)指定斜截面上的应力;(2)主应力大小及主平面位置,并将主平面标在单元体上。

题11-1图

11-2　某点应力状态如题11-2图所示。试求该点的主应力。

11-3　一点处两个互成45°平面上的应力,如题11-3图所示,其中σ未知。试求该点主应力。

题11-2图

题11-3图

11-4　如题11-4图所示,封闭薄壁圆筒的内径d=100mm,壁厚t=2mm,承受内压p=4MPa,外力偶矩Me=0.192kN·m。试求圆筒内壁任一点处的主应力。

11-5　工字形截面梁AB如题11-5图所示,截面的惯性矩Iz=72.56×10-6m4,图中长度单位为mm。求固定端截面翼缘和腹板交界处点a的主应力和主方向。

(www.daowen.com)

题11-4图

题11-5图

11-6　受力体某点平面上的应力如题11-6图所示,求其主应力大小。

11-7　如题11-7图所示,悬臂梁承受载荷F=20kN作用,试绘微体A、B与C的应力图,并确定主应力的大小及方位。

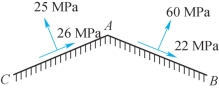
题11-6图

题11-7图

11-8　如题11-8图所示,变形体A四周和底边均与刚性边界光滑接触,上边受均布压力σ0。已知材料的弹性模量E,泊松比μ,求竖直方向和水平方向上的应变和应力。

11-9　如题11-9图所示,矩形板承受正应力σx和σy作用。已知板件厚度δ=10mm,宽度b=800mm,高度h=600mm,正应力σx=80MPa,σy=-40MPa,材料为铝,弹性模量E=70GPa,泊松比μ=0.33。试求板厚的改变量Δδ。

题11-8图

题11-9图

11-10　如题11-10图所示,板件处于纯剪切状态。已知板边切应力为,材料的弹性模量为E,泊松比为μ,试计算板件沿对角线AC与BD方位的正应变ε45°与ε-45°,以及沿板厚的正应变εz。

11-11　如题11-11图所示,在构件表面某点O处,沿0°、45°、90°与135°方位粘贴4个应变片,并测得相应正应变依次为ε0°=450×10-6,ε45°=350×10-6,ε90°=100×10-6与ε135°=100×10-6,判断上述测试结果的可靠性。

题11-10图

题11-11图

11-12　如题11-12图所示,矩形截面杆承受轴向载荷F作用。设截面尺寸b、h以及弹性模量E和泊松比μ均为已知,试计算线段AB的正应变。

题11-12图

11-13　在构件表面某点O处,沿0°、45°与90°方位,粘贴3个应变片,测得该3个方位的正应变分别为ε0°=450×10-6,ε45°=350×10-6与ε90°=100×10-6,该表面处于平面应力状态。已知材料的弹性模量E=200GPa,泊松比μ=0.3,试求该点处的应力σx、σy和xy。

11-14　如题11-14图所示,薄壁圆筒的壁厚δ=10mm、外径D=60mm,在表面A处与其轴线成45°和135°角即xy方向分别贴上应变片。然后在圆筒两端作用外力偶矩Me,已知材料的弹性模量E=200GPa,泊松比μ=0.3,若该圆筒的变形在弹性范围之内,且最大切应力max=80MPa。试求圆筒A处的线应变εx和εy以及变形后筒壁的厚度。

题11-14图

11-15　如题11-15图所示,直径为d的圆截面轴两端承受扭力偶矩M作用。设由试验测得轴表面与轴线成45°方位的正应变ε45°,材料的弹性模量与泊松比分别为E与μ,试求扭力偶矩M之值。

11-16　如题11-16图所示,槽形刚体的宽度和深度都是10mm。在槽内紧密无隙地嵌入一铝质立方块,棱长尺寸是10mm。假设钢块不变形,铝的弹性模量E=70GPa,μ=0.33。当铝块受到压力F=6kN时,试求铝块的3个主应力及相应的应变。

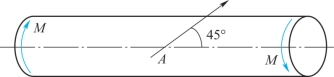
题11-15图

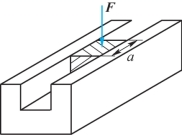
题11-16图

11-17　受内压的薄壁圆筒如题11-17图所示,已知内压为p,平均直径为D,壁厚为t,弹性模量为E、泊松比为μ。试确定圆筒薄壁上任一点的主应力、主应变及第三强度理论、第四强度理论的相当应力。

题11-17图

11-18　试计算题11-9所述板件的体应变、应变能密度与畸变能密度。

11-19　题11-19图中正方形截面棱柱体的弹性模量E、泊松比μ均为已知。试比较在下列两种情况下的相当应力σr3:(1)棱柱体自由受压;(2)棱柱体在刚性方模内受压。

11-20　单元体的应力状态如题11-20图所示,按第三强度理论和第四强度理论求其相当应力。

题11-19图

题11-20图

11-21　如题11-21图所示,外伸梁承受载荷F=130kN作用,许用应力[σ]=170MPa,图中长度单位为mm。试校核梁的强度。如危险点处于复杂应力状态,采用第三强度理论校核强度。

题11-21图

11-22　如题11-22图所示,油管的内径D=11mm,壁厚δ=0.5mm,内压p=7.5MPa,许用应力[σ]=100MPa。试校核油管的强度。

题11-22图

11-23　如题11-23图所示,圆柱形容器受外压p=15MPa作用。材料的许用应力[σ]=160MPa,图中长度单位为mm,试按第四强度理论确定其壁厚。

题11-23图

11-24　如题11-24图所示,车轮由轮毂与套于其上的薄钢圈组成。钢圈的内径d比轮毂的外径D略小,安装时先将钢圈适当加热,以使二者套合,冷却后钢圈即紧套在轮毂上。钢圈的厚度为δ,弹性模量为E,轮毂的刚度很大,分析时可忽略其变形。试求钢圈与轮毂间的相互作用力,以及钢圈横截面上的初应力。

11-25　如题11-25图所示,圆球形薄壁容器的内径为D,壁厚为δ,承受压强为p之内压。试证明壁内任一点处的主应力为σ1=σ2=pD/(4δ),δ3≈0。

题11-24图

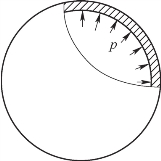
题11-25图

11-26　如题11-26图所示,组合圆环的内、外环分别用铜与钢制成,已知铜环与钢环的壁厚分别为δ1与δ2,交接面的直径为D,铜与钢的弹性模量分别为E1与E2,线胀系数分别为α1与α2,且α1＞α2。试问:温度升高ΔT时,环的周向正应力为何值?

11-27　如题11-27图所示,薄壁圆筒同时承受内压p与扭力偶矩M作用。由试验测得筒壁沿轴向及与轴线成45°方位的正应变分别为ε0°和ε45°,筒的内径D、壁厚δ、材料的弹性模量E与泊松比μ均为已知。试求内压p与扭力偶矩M之值。

题11-26图

题11-27图

11-28　如题11-28图所示,在直径为D=40mm的铝质圆柱体外,光滑套上一壁厚δ=2mm的钢管,圆柱体承受轴向载荷F=40kN作用,铝与钢的弹性模量分别为E1=70GPa与E2=210GPa,泊松比分别为μ1=0.35与μ2=0.25。试计算钢管的周向正应力。

题11-28图