在讨论单向拉伸或压缩时,由各向同性材料在线弹性范围之内的应力应变关系的试验结果,得到单向应力状态下应力与应变的关系是σ=Eε。此外,轴向的变形还将引起径向尺寸的变化,径向应变ε′还可以表示为ε′=-με=-μσ/E。在纯剪切的情况下,试验结果表明,在线弹性范围之内,切应力和切应变之间的关系是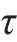 =Gγ。 在最普遍的情况下,描述一点的应力状态需要9个应力分量,如图11-1所示。根据切应力互等定理,在9个应力分量中,独立的应力分量只有6个,即σx、σy、σz和
=Gγ。 在最普遍的情况下,描述一点的应力状态需要9个应力分量,如图11-1所示。根据切应力互等定理,在9个应力分量中,独立的应力分量只有6个,即σx、σy、σz和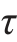 xy、
xy、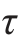 xz、
xz、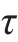 yz。 这种普遍情况可以视为3组单向应力和3组纯剪切的组合。对于各向同性材料,当变形很小且在线弹性范围之内时,线应变只与单向应力有关,而与切应力无关;切应变只与切应力有关,而与正应力无关。
yz。 这种普遍情况可以视为3组单向应力和3组纯剪切的组合。对于各向同性材料,当变形很小且在线弹性范围之内时,线应变只与单向应力有关,而与切应力无关;切应变只与切应力有关,而与正应力无关。
因此,可利用上述关系求出应力分量各自对应的应变,然后进行叠加。例如,在σx、σy、σz共同作用下得到x方向的线应变
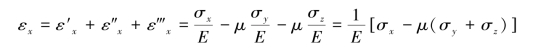
同理,可以求出沿y和z方向的线应变,所以有
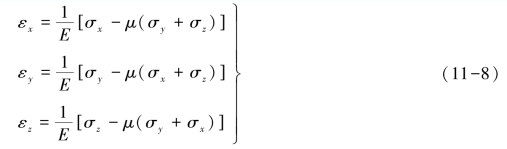
同时,在xy、yz和zx这3个面内的切应变分别为
![]()
式(11-8)和式(11-9)称为一般应力状态下的广义胡克定律。当单元体的3个主应力已知时,广义胡克定律化为
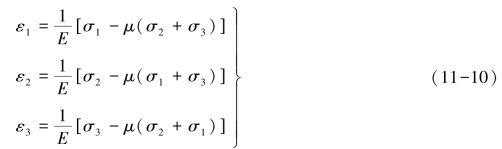
式中,ε1、ε2、ε3分别为沿着正应力σx、σy、σz方向的主应变。此时,3个切应变为0,即γxy=0,γyz=0,γzx=0。
例11-4 图11-8(a)所示的单元体处于平面应力状态,已知应力σx=100MPa,σy=80MPa,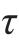 xy=50MPa,弹性模量E=200GPa,泊松比μ=0.3,试求正应变εx、εy与切应变γxy,以及α=30°方位的正应变ε30°。
xy=50MPa,弹性模量E=200GPa,泊松比μ=0.3,试求正应变εx、εy与切应变γxy,以及α=30°方位的正应变ε30°。
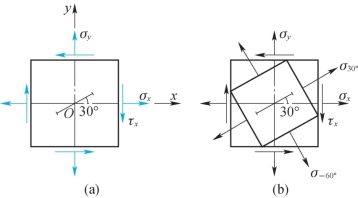
图11-8
解:根据广义胡克定律,得
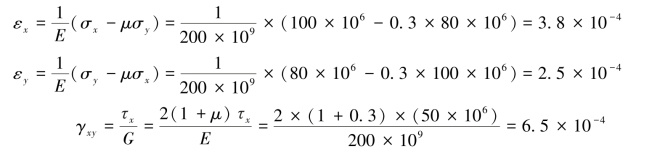
斜截面的应力如图11-8(b)所示,则
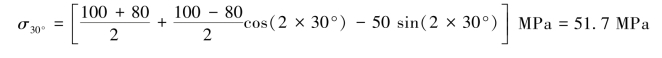
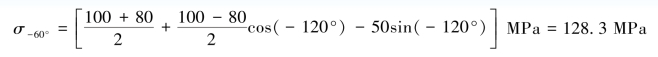
根据广义胡克定律,得30°的正应变为
![]()
例11-5 构件表层一点处的应力如图11-9(a)所示,为了测量应力,在该点沿0°、45°与90°粘贴3个应变片,测得相应正应变依次为ε0°,ε45°与ε90°, 如图11-9(b)所示。已知材料的弹性模量为E,泊松比为μ,试根据上述测试应变值,确定该点处的正应力σx,σy与切应力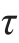 x。
x。
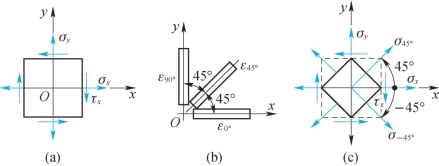
图11-9
解:当α=45°与α=-45°时,相应截面的正应力分别为(www.daowen.com)
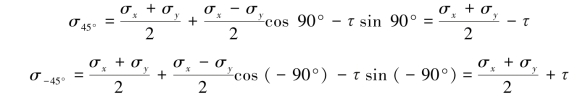
根据广义胡克定律,45°方位的正应变为
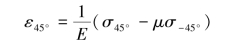
由此得
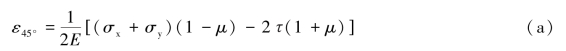
根据广义胡克定律还可知,沿0°与90°方位的正应变分别为

联立求解式(a)、式(b)与式(c),于是得
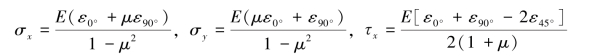
将测试值ε0°,ε45°与ε90°,代入上述方程,即可确定相应正应力σx、σy与切应力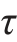 xy。
xy。
例11-6 在建立圆轴扭转切应力公式时,曾提出若干假设,试根据该假设说明圆轴轴向横截面与径向纵截面上均无正应力。
解:根据各横截面仍保持平面,其形状、大小均不改变,如同刚性圆片这一假设可得(这里采用圆柱坐标)
![]()
式中,下标ρ和φ分别代表圆轴的径向和环向。
又据横截面间的距离均不改变这一假设可得
![]()
依据圆柱坐标系中的广义胡克定律,有
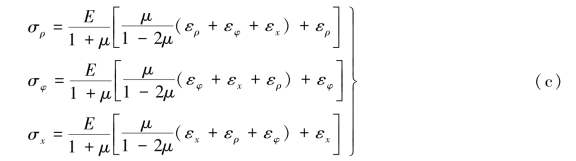
将式(a)和式(b)代入式(c),得到
σρ=0,σφ=0,σx=0
这就说明圆轴轴向横截面与径向纵截面(及同心圆柱面)上均无正应力。
思政提示
相较于单向应力状态下的胡克定律,广义胡克定律更加全面地揭示了各方向的应力和应变之间的关系。我们看待事物时,不要只看其中一方面,而是要从不同的角度观察其多面性,同时也要善于发现事物各个方面之间的联系。只有这样才能将问题看全面,将事情做得周到。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







