1)双向应力状态单元体与应力圆的对应关系
首先是点面对应关系,应力圆上某一点的坐标值对应着单元体某一截面上的正应力和切应力值。其次是二倍角对应关系,单元体上任意两个斜截面的外法线之间的夹角若为α,则对应在应力圆上代表该斜截面上应力的两点之间的圆弧所对应的圆心角为2α。最后是转向对应关系,应力圆的半径旋转时,半径端点的坐标随之改变,对应地,单元体上斜截面的法线亦沿相同方向旋转,这样才能保证斜截面上的应力与应力圆上半径端点的坐标相对应。
2)确定单元体斜截面上的应力
根据以上对应关系,可以从应力圆上确定单元体内任意斜截面上的应力值。在图11-6中,若求法线n与x轴夹角为逆时针α角的斜截面的应力σα、 α,则在应力圆上,从点D也按逆时针方向沿圆周转到点E,且弧DE所对应的圆心角为2α,则点E的坐标就代表以n为法线的斜面上的应力σα、
α,则在应力圆上,从点D也按逆时针方向沿圆周转到点E,且弧DE所对应的圆心角为2α,则点E的坐标就代表以n为法线的斜面上的应力σα、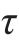 α。有
α。有
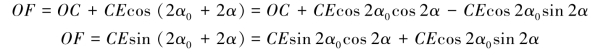
因为
![]()
所以

这就是式(11-1)和式(11-2)。(https://www.daowen.com)
3)主应力的数值和主平面的方位
由于应力圆上点A1的横坐标(正应力)最大,纵坐标(切应力)等于0,所以点A1的横坐标代表最大主应力,即σmax=OA1=OC+CA1。同理,点B1的横坐标表示最小正应力,即σmin=OB1=OC-CB1。OC是应力圆的圆心横坐标,而CA1和CB1都是应力圆的半径,则得到式(11-4)。在应力圆上有点D到点A1所对应的圆心角为顺时针的2α0,在单元体中由x轴也顺时针量取α0,这就确定了σmax所在平面的法线位置,按照关于α的符号规定,顺时针的α0是负的,2α0应为负值,所以得到式(11-3)。
4)确定最大切应力及其作用平面位置
由应力圆可知,G1和G2两点的纵坐标分别代表最大和最小切应力。因为CG1和CG2都是应力圆的半径,故得式(11-6)。在应力圆上,由点A1到点G1所对圆心角为逆时针的π/2,所以在单元体内,最大切应力所在平面与σmax所在主平面的夹角为逆时针的π/4。也可以在应力圆上直接标出主应力的方向、主平面的位置和最大切应力平面的方向。
例11-3 试用图解法求解图11-7所示的应力状态单元体的主应力。

图11-7
解:首先,根据选定坐标系的比例尺,由坐标(200,-300)和(-200,300)分别确定点C和点C′,如图11-7(b)所示。然后,以![]() 为直径画圆,即得相应的应力圆。从应力圆量得主应力及方位角,并画出主应力的应力状态如图11-7(c)所示。得到σ1=360MPa,σ2=0,σ3=-360MPa,α1=28°,
为直径画圆,即得相应的应力圆。从应力圆量得主应力及方位角,并画出主应力的应力状态如图11-7(c)所示。得到σ1=360MPa,σ2=0,σ3=-360MPa,α1=28°,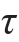 max=360MPa。
max=360MPa。
思政提示
相较于解析法,图解法是在一种更加形象直观的视角下进行应力状态分析,在某种程度上使应力状态分析过程更简便。我们在解决问题时,也应善于从不同的视角去分析看待问题,利用恰当的方法往往可以事半功倍。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





