为了求得切应力的极值及其所在平面的方位,将式(11-2)对α求导,得

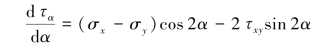
若α=α1时,上式等于0,则在α1所确定的截面上切应力为极值。将α1代入上式并令其等于0,求得

由式(11-5)也可以确定两个相互垂直的平面,在这两个平面上分别作用着最大或最小切应力。由式(11-5)解出α1代入式(11-2),求得切应力的最大值和最小值

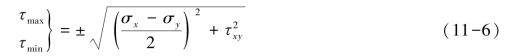
与正应力的极值和所在两个平面方位的对应关系相似,切应力的极值于所在两个平面方位的对应关系是:若则绝对值较小的α1对应最大切应力所在的平面。

比较式(11-3)和(11-5),可以得到tan2α0=-即极值切应力所在的平面的外法线与主平面的外法线之间的夹角为45°。

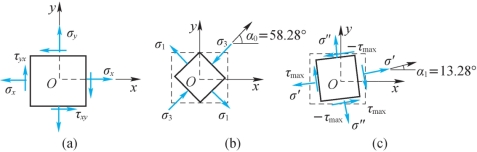
例11-1　某点的应力状态如图11-4(a)所示,已知σx=30MPa,σy=10MPa,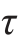xy=20MPa。试求:(1)主应力及主平面方向;(2)最大、最小切应力。

解:(1)主应力由式(11-4)得出,即

在垂直于z轴的前后两面上无切应力,其也是主平面,且主应力大小为0。3个主应力按代数值的大小排列,有σ1=42.36MPa;σ2=0;σ3=-2.36MPa。

主平面方向角由式(11-3)确定,即

解得α0=-31.72°,故两个主平面外法线与x轴的夹角分别为58.28°和148.28°,如图11-4(b)所示。

(2)最大、最小切应力。将题目中σx、σy、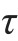xy各应力代入式(11-6),即可求得最大、最小切应力。若应力状态由主应力表示,则式(11-6)写成为

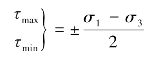
所以,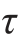max=[42.36-(-2.36)]/2MPa=22.36MPa,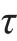min=-22.36MPa。

(www.daowen.com)

图11-4

讨论:极值切应力作用平面与主平面间的夹角为45°,故α1=13.28°或103.28°。在α1=13.28°的平面上,切应力由式(11-2)给出,即

注意,在α1=13.28°的平面上,还有正应力,且由式(11-1)可知:

故在α1=13.28°的平面上,σ′=20MPa,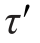=22.36MPa;同样,可求得在α1=103.28°的平面上,σ″=20MPa,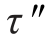=-22.36MPa,如图11-4(c)所示。值得指出的是,由上例可知有:σx+σy=σ1+σ3=σ′+σ″,即讨论一点的应力状态时,过该点任意两个相互垂直平面上的正应力之和是不变的。在平面应力状态下,这一结论可由式(11-5)直接得到。在三向应力状态下,可以进一步写为:J=σx+σy+σz=σ1+σ2+σ3,式中J表示一点应力状态的第一不变量,即过该点任意3个相互垂直平面上的正应力之和是不变的。

例11-2　已知圆轴如图11-5所示,直径d=15mm,在外力偶矩Me=100N·m作用下,发生扭转。试分析圆轴表面上点A的应力状态,并分析铸铁试件受扭时的破坏现象。

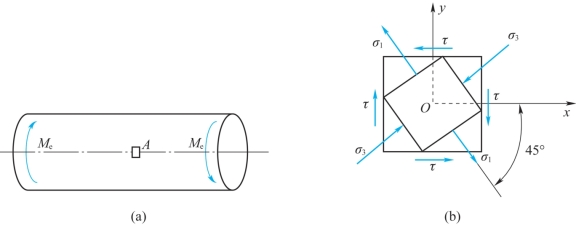
图11-5

解:(1)点A处横截面上的切应力为

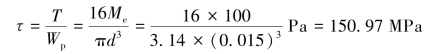
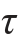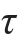在点A周围截取单元体,单元体各面上的应力如图11-5(b)所示,σx=σy=0,xy=,所以

(2)主应力为σ1=150.97MPa,σ2=0,σ3=-150.97MPa。　由

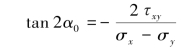
得主平面位置为α0=-45°或α0=-135°,如图11-5(b)所示。

(3)由以上分析可知,低碳钢试件扭转时的屈服现象是材料沿截面产生滑移的结果,最后沿截面断开,这说明低碳钢扭转破坏是截面上最大切应力作用的结果,即对于低碳钢这种塑性材料来说,其抗剪能力小于抗拉或抗压能力。铸铁试件扭转时,大约沿与轴线成45°螺旋线断裂,说明是最大拉应力作用的结果,即对于铸铁这种脆性材料来说,其抗拉能力小于抗剪和抗压能力。

思政提示

对应力状态进行分析时,我们主要关注正应力与切应力的极值及极值所在平面的位置。我们在做事时,也应该尝试去找到事物的“极值”,要善于抓住事物最突出的特点,这样有助于我们将问题分析透彻,将事情做好。