前面所研究的梁均为静定梁。在实际工程中,有时为了提高梁的强度与刚度,或由于构造上的需要,往往给静定梁再增加约束,于是,梁的支反力(包括支反力偶)的数目超过有效平衡方程的数目,即成为超静定梁(静不定梁)。例如,在图10-12(a)中,车削工件的左端由卡盘夹紧。对细长的工件,为了减少变形,提高加工精度,在工件的右端又安装尾顶针。把卡盘夹紧的一端简化成固定端,尾顶针简化为铰支座。在切削力F作用下,得计算简图如图10-12(b)所示。这样便有FRAx,FRAy,MA,FRBy等4个约束反力,而可以利用的静力平衡方程只有3个,即

因为由3个平衡方程不能解出全部4个未知力,所以这是一个超静定梁。

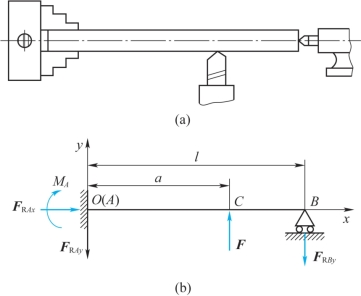
图10-12

在超静定梁中,凡是多于维持平衡所必需的约束称为多余约束,与其相应的支反力或支反力偶矩统称为多余支反力。显然,超静定梁的超静定度等于多余约束或多余支反力的数目。例如,图10-13(a)、(b)所示梁分别为一度超静定梁与两度超静定梁。

图10-13

解超静定梁的步骤如下:

(1)用多余约束反力代替多余约束(取相当系统,原则:便于计算);

(2)在多余约束处根据变形协调条件列出变形的几何方程;

(3)把物理条件代入几何方程列出力的补充方程求出多余约束反力;

(4)计算梁的内力、应力、变形、强度、刚度。

下面举例说明分析超静定梁的方法。

例10-4　如图10-14所示,已知梁的EI、长度,求各约束反力。

图10-14

解:研究对象为AB梁,对其进行受力分析,并建立静力学平衡方程

因为平衡方程数量小于需要求解的未知约束反力的数量,所以该问题为超静定问题。

(1)建立相当系统(去掉C支座)。

去掉多余约束并保留约束反力而成为形式上的静定结构——相当系统,如图10-15所示。

图10-15

(2)列出变形协调方程。

在上述相当系统中,将约束反力FC视为载荷,设均布载荷q单独作用时在点C处产生的挠度为wCq,约束力FC单独作用时在点C处产生的挠度为,如图10-16所示,则有

图10-16

(3)物理条件。

分别计算上述两个单独作业时产生的挠度

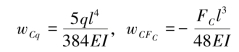
(4)联立方程求解

由以上分析可得

例10-5　试求图10-17所示超静定梁支座约束反力值,梁弯曲刚度EI为常量。

图10-17

解:如图10-18所示,去掉支座C,取简支梁AB为相当系统。

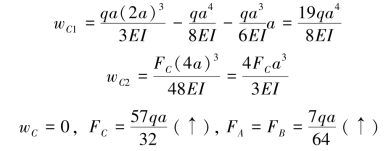
如图10-19所示,利用对称性取C端固定,以AC段悬梁比拟作基本系统,wA=0。

图10-18

图10-19(www.daowen.com)

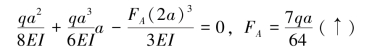
例10-6　试用积分法求图10-20所示超静定梁的支座约束反力值,梁弯曲刚度EI为常量。

图10-20

解:

联立求解得

思政提示

通过合理增加约束的数量,静定梁可以转变为超静定梁,这样会降低梁的挠度,提高梁抵抗弯曲的能力。“一个好汉三个帮”“落篱之下,独木成林,焉能存根”就是这样的道理,只有团结协作、齐心协力才能最终成功。在今天的行业竞争中,同行、同企业之间的互相竞争是同行关系的主旋律。其实,换一种思维,合作双赢、相互支撑才是达到目的的最好选择。

习　题

10-1　如题10-1图所示各梁,弯曲刚度EI均为常数。

(1)试根据梁的弯矩图与支持条件画出挠曲轴的大致形状;

(2)利用积分法计算梁的最大挠度与最大转角。

题10-1图

10-2　如题10-2图所示各梁,弯曲刚度EI均为常数。

(1)试写出计算梁位移的边界条件与连续条件;

(2)试根据梁的弯矩图与支持条件画出挠曲轴的大致形状。

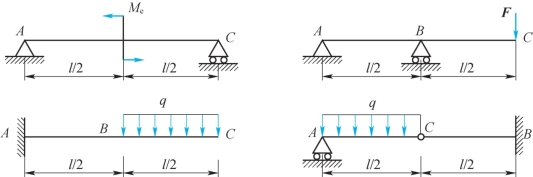
题10-2图

10-3　如题10-3图所示各梁,弯曲刚度EI均为常数,试用叠加法计算截面B的转角与截面C的挠度。

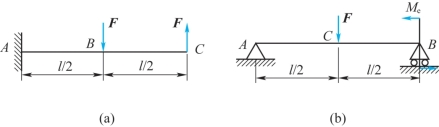
题10-3图

10-4　如题10-4图所示外伸梁,两端承受载荷F作用,弯曲刚度EI为常数,试问:

(1)当x/l为何值时,梁跨度中点的挠度与自由端的挠度数值相等;

(2)当x/l为何值时,梁跨度中点的挠度最大。

10-5　试计算题10-5图所示钢架截面A的水平与铅垂位移,设弯曲刚度EI为常数。

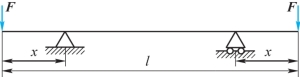
题10-4图

题10-5图

10-6　试用叠加法计算题10-6图所示各阶梯梁的最大挠度,设惯性矩I2=2I1。

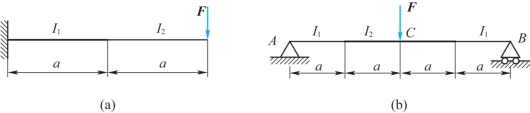
题10-6图

10-7　一跨度l=4m的简支梁如题10-7图所示,受集度q=10kN/m的均布载荷和P=20kN的集中载荷作用。梁由两槽钢组成。设材料的许用应力[σ]=160MPa,梁的许用挠度[w]=1/400。试选定槽钢的型号,并校核其刚度。梁的自重忽略不计。

题10-7图

10-8　试求题10-8图所示梁的支反力,并画剪力图和弯矩图,设弯曲刚度EI为常数。

10-9　如题10-9图所示结构,悬臂梁AB与简支梁DG均用18工字钢制成,BC为圆截面钢杠,直径d=20mm,梁与杆的弹性模量均为E=200GPa,图中长度单位为m。若载荷F=30kN,试计算梁与杆内的最大应力,以及横截面C的铅垂位移。

题10-8图

题10-9图