由前述分析可知,在小变形且梁内应力不超过材料的比例极限时,挠曲轴近似微分方程为

它是一个线性微分方程。由前述分析还可知,在小变形的条件下,由于截面形心的轴向位移可以忽略不计,因此梁内任一截面的弯矩与载荷成线性齐次关系。

设梁上作用着n种载荷,第一种载荷引起的弯矩为M1(x),挠度为w1(x);第二种载荷引起的弯矩为M2(x),挠度为w2(x);第n种载荷引起的弯矩为Mn(x),挠度为wn(x)。由于在上述条件下,内力弯矩与载荷也是线性关系。所以,n种载荷共同作用时所引起的弯矩为M(x)=M1(x)+M2(x)+…+Mn(x)。

当n种载荷单独作用时挠曲轴的微分方程分别为

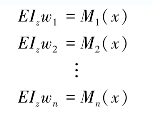
将以上n个式子相加,得

EIz(w1+w2+…+wn)=M1(x)+M2(x)+…+Mn(x)=M(x)

另外,当n种载荷同时作用时挠曲轴的微分方程为

EIzw=M(x)

比较单独和同时作用的结果,得

w(x)=w1(x)+w2(x)+…+wn(x)

q(x)=q1(x)+q2(x)+…+qn(x)

这就证明了求挠度或转角的叠加原理:在材料服从胡克定律和小变形情况下,梁上有几种载荷共同作用时的挠度或转角,等于几种载荷分别单独作用时的挠度或转角之代数和。

为了叠加方便,现将梁在简单载荷作用下的变形汇总于表10-1中,以便直接查用。

表10-1

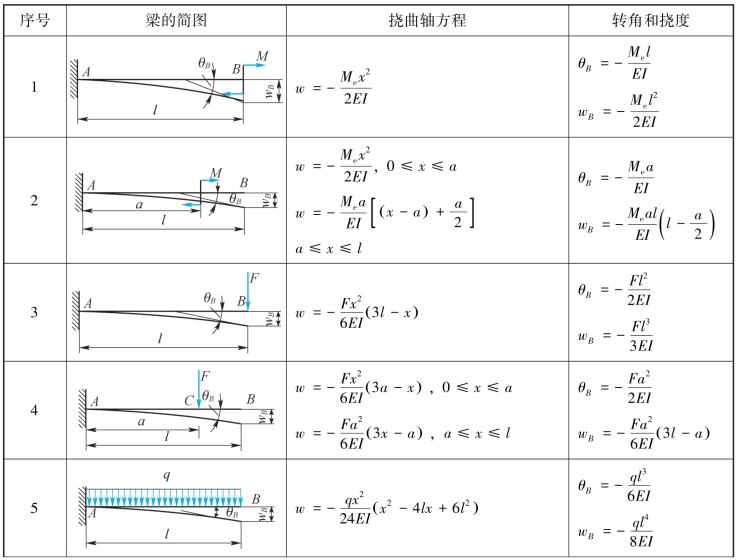
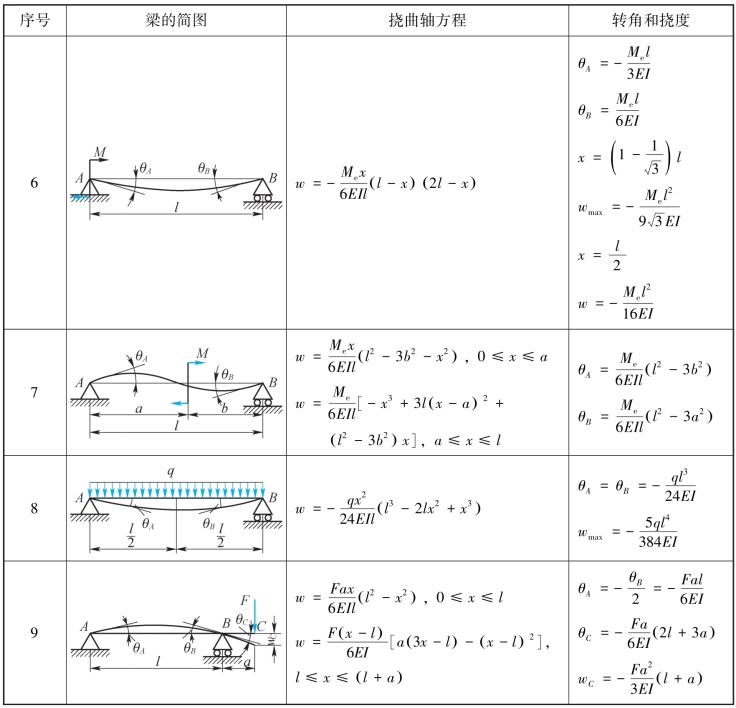
续表

例10-2　用叠加法求图10-7所示外伸梁的θC和wC,　梁的抗弯刚度是EI。(www.daowen.com)

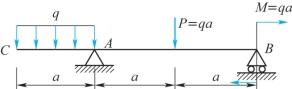
图10-7

解:使用叠加积分法求转角和挠度。

(1)将梁上的载荷分解为3种简单载荷单独作用的情形,如图10-8(a)、　(b)、(c)所示。

θC=θC(a)+θC(b)+θC(c)

wC=wC(a)+wC(b)+wC(c)

(2)而第三种情形又可分解为图10-8(d)、(e)2种载荷单独作用的情形。

θC(c)=θC(d)+θC(e)

wC(c)=wC(d)+wC(e)

图10-8

(3)应用挠度表确定3种情况下,梁的点C处的转角和挠度。

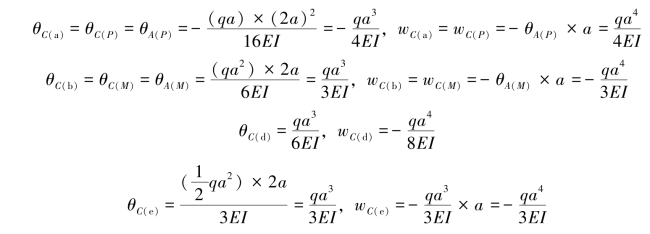
而对于第三种情形下2种载荷单独作用时,应用叠加法进行叠加。

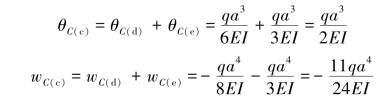
(4)应用叠加法,将3种情形下转角和挠度叠加。

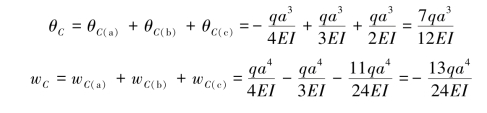
思政提示

复杂载荷作用下梁的弯曲结果,可以视为多个简单弯曲的叠加。同样,在生活中应当注意“勿以恶小而为之,勿以善小而不为”,不要因为是件小的坏事就去做,不要因为是件小的善事就毫不关心,如果不能处理好一件件小事,就有可能导致其相互叠加,最终产生不可预料的结果,导致难以计量的损失和影响。