1)弯曲正应力强度条件

最大弯曲正应力发生在横截面上离中性轴最远的各点处,而该处的切应力一般为0或很小,因此最大弯曲正应力作用点可看成是处于单向受力状态,则弯曲正应力强度条件为

即要求梁内的最大弯曲正应力σmax不超过材料在单向受力时的许用应力[σ]。对于等截面直梁,上式变为

式(9-27)与式(9-28)仅适用于许用拉应力[σt]与许用压应力[σc]相同的梁,如果二者不同,如灰口铸铁等脆性材料的许用压应力大于许用拉应力,则应按拉伸与压缩分别进行强度计算。

2)弯曲切应力强度条件

最大弯曲切应力通常发生在中性轴上各点处,而该处的弯曲正应力为0,因此最大弯曲切应力作用点处于纯剪切状态,则相应的强度条件为

即要求梁内的最大弯曲切应力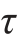max不超过材料在纯剪切时的许用切应力[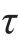]。对于等截面直梁,上式变为

前面曾经指出,在一般细长的非薄壁截面梁中,最大弯曲正应力远大于最大弯曲切应力。因此,对于一般细长的非薄壁截面梁,通常按弯曲正应力强度条件进行分析即可。但是,对于薄壁截面梁与弯矩较小而剪力却较大的梁(如短而高的梁、集中载荷作用在支座附近的梁等),则不仅应考虑弯曲正应力强度条件,还应考虑弯曲切应力强度条件。

例9-4　起吊重量为50kN的单梁吊车,其跨度l=10.5m,由45a工字钢制成,其计算简图如图9-18(a)所示。现拟将其起吊重量提高到Q=70kN,试校核梁的强度。若强度不够,再计算其可能承受的起吊重量。梁的材料许用应力[σ]=140MPa;电葫芦自重G=15kN,暂不考虑梁的自重。

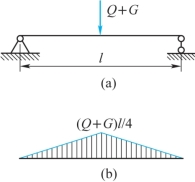
图9-18

解:(1)作弯矩图,确定危险截面。

显然,当电葫芦行至梁中点时所引起的弯矩最大,如图9-18(b)所示。由弯矩图可知,危险截面为中点处的截面,即

(2)计算最大弯曲正应力。

由于是等截面梁,且截面(如工字钢、矩形、圆形)关于中性轴对称,因此最大弯曲正应力发生在危险截面(最大弯矩处)的上下边缘点处。

由型钢表查得45a工字钢的抗弯截面模量Wz=1430cm3。

故梁内最大工作正应力为

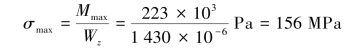
(3)依据强度条件,进行强度计算。

显然,最大工作应力超过了材料的许用应力,故梁不安全。(www.daowen.com)

梁的最大承载能力为

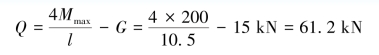
因此,梁的最大起吊重量为61.2kN。

例9-5　图9-19(a)所示简支梁,受均布载荷q作用,梁跨度l=2m,[σ]=140MPa,q=2kN/m,试按以下两个方案设计轴的截面尺寸,并比较质量。分别考虑两种情况:(1)实心圆截面梁;(2)空心圆截面梁,其内、外径之比α=0.9。

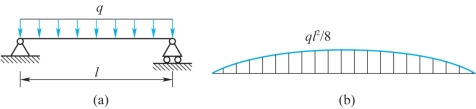
图9-19

解:画梁的弯矩图如图9-19(b)所示,由弯矩图可知,梁中点截面为危险截面,其上弯矩为

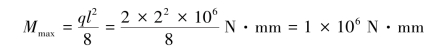
(1)设计实心截面梁的直径d。

依据强度条件

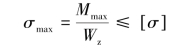
将Wz=代入上式得

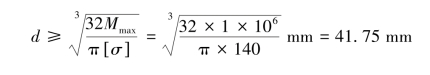
取d=42mm。

(2)确定空心截面梁的内、外径d1及D。

将Wz=(1-α4)代入强度条件得

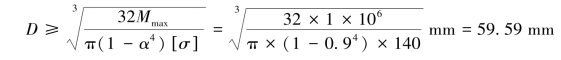
取D=60mm,则d1=0.9D=54mm。

(3)比较两种不同截面梁的质量。

因材料及长度相同,故两种截面梁的质量之比等于其截面积之比,即

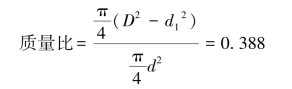
上面计算结果表明,空心截面梁的质量比实心截面梁的质量小很多。因此,在满足强度要求的前提下,采用空心截面梁可节省材料、减轻结构质量。

还应指出,在某些薄壁梁的某点处,如工字形截面的腹板和翼缘的交界处,弯曲正应力与弯曲切应力可能均具有相当大的数值,这种正应力与切应力联合作用下的强度问题,本书不详细展开讨论。