首先讨论工字形截面梁腹板上的切应力。腹板截面是一个狭长矩形,关于矩形截面上切应力分布的两个假设仍然适用。用相同的方法,必然导出相同的切应力计算公式,即

式中,b0为腹板宽度。若需要计算腹板上距中性轴为y处的切应力,则 为图9-17(a)中画阴影线部分的面积对中性轴的静矩,即
为图9-17(a)中画阴影线部分的面积对中性轴的静矩,即

于是
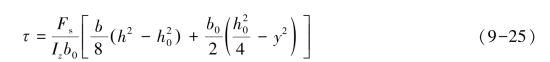

图9-17(https://www.daowen.com)
可见,沿腹板高度,切应力也是按抛物线规律分布的,如图9-17(b)所示。将y=0和y=±h0/2分别代入式(9-25),求得腹板上的最大和最小切应力分别是

从以上两式看出,因为腹板的宽度b0远小于翼缘的宽度b,所以 max与
max与 min实际上相差不大,可以认为在腹板上切应力大致是呈均匀分布的。若以图9-17(b)中应力分布图的面积乘以腹板厚度b0,即可得到腹板上的总剪力Fs1。计算结果表明,Fs1= (0.95~0.97)Fs。可见,横截面上的剪力Fs的绝大部分由腹板所负担。由于腹板几乎负担了截面上的全部剪力,而且腹板上的切应力又接近于均匀分布,因此可用腹板的截面面积除剪力Fs,近似地得出腹板内的切应力,即
min实际上相差不大,可以认为在腹板上切应力大致是呈均匀分布的。若以图9-17(b)中应力分布图的面积乘以腹板厚度b0,即可得到腹板上的总剪力Fs1。计算结果表明,Fs1= (0.95~0.97)Fs。可见,横截面上的剪力Fs的绝大部分由腹板所负担。由于腹板几乎负担了截面上的全部剪力,而且腹板上的切应力又接近于均匀分布,因此可用腹板的截面面积除剪力Fs,近似地得出腹板内的切应力,即

在翼缘上,虽然也应有平行于Fs的切应力分量,但分布情况比较复杂,数量很小,并无实际意义,所以通常不进行计算。此外,翼缘上还有平行于翼缘宽度b的切应力分量。它与腹板内的切应力比较,一般来说也是次要的。
同时也注意到,工字梁翼缘的全部面积都在离中性轴最远处,每一点的正应力都比较大,所以翼缘负担了截面上的大部分弯矩。
思政提示
弯曲切应力是由剪力导致的,其分布趋势与弯曲正应力相反。应当正确看待经验和实践的关系,可以用经验指导和改进工作,但是不应当盲从盲信,以经验为出发点探索当前问题的解决方法。组织严密、科学合理的实践,仍然是检验结论和方法的不二法门。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






