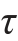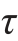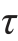在图9-14(a)所示的矩形截面梁的任意截面上,剪力Fs皆与截面的对称轴y重合。关于横截面上切应力的分布规律,作以下两个假设:(1)横截面上各点的切应力的方向都平行于剪力Fs;(2)切应力沿截面宽度均匀分布。在截面高度h大于宽度b的情况下,以上述假定为基础得到的解,与精确解相比有足够的精确度。按照这两个假设,在距中性轴为y的横线pq上,各点的切应力都相等,且都平行于Fs。再由切应力互等定理可知,在沿pq切出的平行于中性层的pr平面上,也必然有与相等的′,如图9-15所示,而且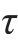′沿宽度b也是均匀分布的。

如以横截面m—n和m1—n1从图9-14(a)所示梁中取出长为dx的一段,如图9-15(a)所示,设截面m—n和m1—n1上的弯矩分别为M和M+dM。以平行于中性层且距中性层为y的pr平面从这一段梁中截出一部分prnn1,则在这一截出部分的左侧面rn上,作用着因弯矩M引起的正应力;而在右侧面pn1上,作用着因弯矩M+dM引起的正应力。在顶面pr上,作用着切应力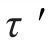。以上3种应力(即两侧正应力和顶面切应力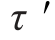)都平行于x轴。如图9-15(b)所示,在右侧面pn1上,由微内力σdA组成的内力系的合力为

式中,A1为侧面pn1的面积。

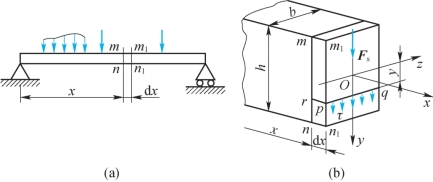
图9-14

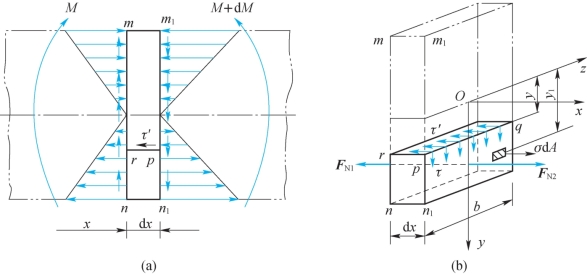
图9-15

正应力σ应按公式计算,于是

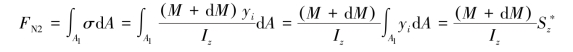
式中

是横截面的部分面积A1对中性轴的静矩,也就是距中性轴为y的横线pq以下的面积对中性轴的静矩。同理,可以求得左侧面rn上的内力系合力FN1为

在顶面rp上,与顶面相切的内力系的合力为

FN2,FN1和dFs′的方向都平行于x轴,应满足平衡方程∑Fx=0,即FN2-FN1-dFs′=0,将FN2,FN1和dFs′的表达式代入上式,得

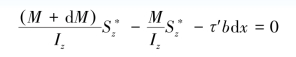(www.daowen.com)

简化后得出

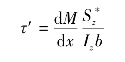
由式(8-2),有=Fs,于是上式化为

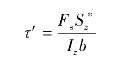
式中,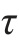′是距中性层为y的pr平面上的切应力,由切应力互等定理,它等于横截面的横线pq上的切应力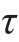,即

式中,Fs为横截面上的剪力,b为截面宽度,Iz为整个截面对中性轴的惯性矩,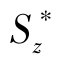为截面上距中性轴为y的横线以下部分的面积对中性轴的静矩。这就是矩形截面梁弯曲切应力的计算公式。

如图9-16(a)所示,对于矩形截面,可取dA=bdy1,于是式(9-21)化为

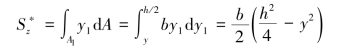
这样,式(9-22)可以写成

从式(9-23)可以看出,沿截面高度方向切应力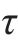按抛物线规律变化,如图9-16(b)所示。当y=±这表明在截面上、下边缘的各点处,切应力等于0。随着离中性轴的距离y的减小,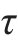逐渐增大。当y=0时,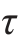为最大值,即最大切应力发生于中性轴上,且

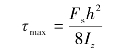
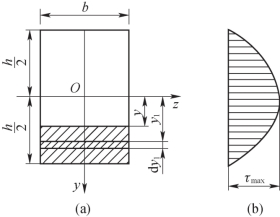
图9-16

将Iz=代入上式,即可得出

可见,矩形截面梁的最大切应力为平均切应力的1.5倍。