由上述分析可以看出,要计算截面对某坐标轴z的惯性矩,首先需要计算各组成部分对该轴的惯性矩。然而,在很多情况下,各组成部分本身的形心轴z0与z轴并不重合,如图9-8所示。因此,需要确定同一截面对于上述两平行轴的两个惯性矩之间的关系。

如图9-9所示,设z0轴为形心轴,z轴与z0轴平行,相距为a,微面积dA在y-z与y0-z0坐标系中的纵坐标分别为y与y0,则由式可知,截面对z轴的惯性矩为

式中,右端第一项代表截面对形心轴z0的惯性矩即Iz0;至于第二项,由于z0轴通过截面形心,积分应为0,因此得出结论

即截面对于任一坐标轴z的惯性矩,等于对其平行形心轴z0的惯性矩加上截面面积与两轴间距离平方之乘积。此定理称为惯性矩平行轴定理。利用此定理,即可由Iz0计算Iz,也可由Iz计算Iz0。

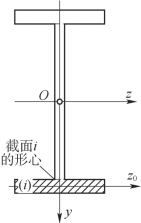
图9-8

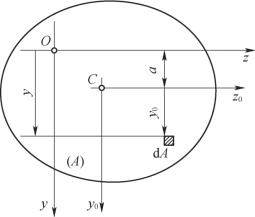
图9-9

例9-2　求图9-10(a)所示铸铁悬臂梁内最大拉应力及最大压应力,梁的横截面如图9-10(b)所示。P=20kN,Iz=10200cm4。

解:(1)画弯矩图,确定危险面。

因为梁是等截面的,且横截面相对z轴不对称,铸铁的抗拉能力与抗压能力又不同,故绝对值最大的正、负弯矩所在面均可能为梁的危险面。弯矩图如图9-11所示。

图9-10

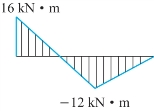
图9-11

(2)确定危险点,计算最大拉应力与最大压应力。

由弯矩图看出,A、B两截面均可能为危险面。截面A上有最大正弯矩,该截面下边缘各点处将产生最大拉应力,上边缘各点处将产生最大压应力;而截面B上有最大负弯矩,该截面下边缘各点处将产生最大压应力,上边缘各点处将产生最大拉应力。A、B截面正应力分布如图9-12所示。

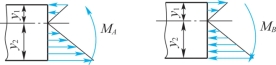
图9-12(www.daowen.com)

显然,截面A上的最大拉应力要大于截面B上的最大拉应力,故梁内最大拉应力发生在截面A上边缘各点处,其值为

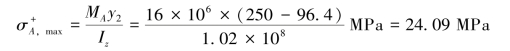
对A、B两截面下边缘各点处正应力,需经计算才能得知哪个截面上的最大压应力更大

由此可见,梁内最大压应力发生在截面B的下边缘各点处。

例9-3　宽度b=6mm、厚度δ=2mm的钢带,环绕在直径D=1400mm的带轮上,如图9-13所示。已知钢带的弹性模量E=200GPa,试求钢带内的最大弯曲正应力与钢带承受的弯矩。

图9-13

解:(1)应力分析。

在与带轮贴合的钢带部分,其轴线的曲率半径为

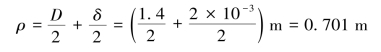
横截面上离中性轴最远点的纵坐标为

所以,钢带内的最大弯曲正应力为

(2)内力分析。

由式(9-9)可知,钢带承受的弯矩为

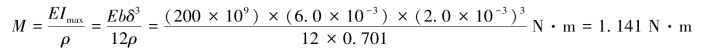
思政提示

组合截面可以视为由多个简单截面构成,其惯性矩也可通过平行轴公式由多个简单截面的惯性矩算得。同样,国家也是由一个个的个体所组成,我们只有充分了解国家和民族的发展重心和方向,将自己的理想和追求统一到民族复兴、国家富强的道路上来,才能更好地实现自身的价值,做出应有的贡献。