设在梁的纵向对称面内,作用大小相等、方向相反的力偶,构成纯弯曲。这时,梁的横截面上只有弯矩,因而只有与弯矩相关的正应力。像研究扭转一样,研究纯弯曲时的正应力也是从综合考虑几何、物理和静力等三方面关系入手。

(1)几何关系。弯曲变形前和变形后的梁段分别如图9-3(a)、(b)所示。以梁横截面的对称轴为y轴,并规定向下为正如图9-3(c)所示。以中性轴为z轴,但中性轴的位置尚待确定。在中性轴尚未确定之前,只能暂时认为其是通过原点的横截面的法线。根据平面假设,变形前相距为dx的两个横截面,变形后各自绕中性轴相对旋转了一个角度dθ,如图9-3(b)所示,并仍保持为平面。这就使得距中性层为y的纤维bb的长度变为

这里ρ为中性层的曲率半径。纤维bb的原长度为dx,且bb=dx=OO。因为变形前和变形后中性层内纤维OO的长度不变,故有

根据应变的定义,求得纤维bb的应变为

可见,纵向纤维的应变与它到中性层的距离成正比。

(2)物理关系。因为纵向纤维之间无正应力,所以每一纤维都受单向拉伸或压缩。当应力小于比例极限时,由胡克定律知

σ=Eε

将式(9-1)代入上式,得

这表明,任意纵向纤维的正应力与它到中性层的距离成正比。在横截面上,任意点的正应力与该点到中性轴的距离成正比。亦即沿截面高度,正应力按直线规律变化,且在中性层处等于零,如图9-3(d)所示。

(3)静力关系。横截面上的微内力σdA组成垂直于横截面的空间平行力系(在图9-3(c)中,只画出力系中的一个微内力σdA),这一力系只可能简化成3个内力分量,即平行于x轴的轴力FN,分别对y轴和z轴的力偶矩Miy和Miz,表达式分别为

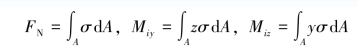
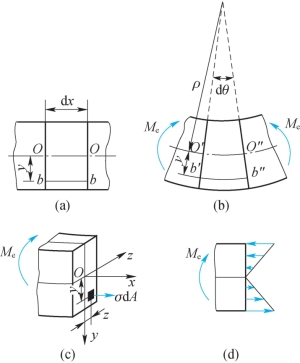
图9-3

横截面上的内力应与截面左侧的外力平衡。在纯弯曲情况下,截面左侧的外力只有对z轴的力偶矩Me,如图9-3(c)所示。由于内、外力必须满足平衡方程∑Fx=0和∑My=0,故有FN=0和Miy=0,即

这样,横截面上的内力系最终只归结为一个力偶矩Miz,也就是弯矩M,即

根据平衡方程,弯矩M与外力偶矩Me大小相等,方向相反。

下面对式(9-3)　～式(9-5)作进一步讨论,将式(9-2)代入式(9-3),得(www.daowen.com)

式中,E/ρ为常量,不等于0,故必须有∫AydA=Sz=0,即横截面对z轴的静矩必须等于0,亦即z轴(中性轴)应通过截面形心,这就完全确定了z轴和x轴的位置。中性轴通过截面形心又包含在中性层内,所以梁截面的形心连线(轴线)也在中性层内,其长度不变。将式(9-2)代入式(9-4),得

式中,∫AyzdA=Iyz是横截面对y和z轴的惯性积。由于y轴是横截面的对称轴,必然有Iyz=0,因此式(9-7)是自动满足的。将式(9-2)代入式(9-5),得

式中,是横截面对z轴(中性轴)的惯性矩。于是式(9-8)可以写成

式中,是梁轴线变形后的曲率。上式表明,EIz越大,则曲率越小,故EIz称为梁的抗弯刚度。联立式(9-2)和式(9-9)消去,得

这就是纯弯曲时正应力的计算公式。对图9-3所取坐标系,在弯矩M为正的情况下,y为正时,σ为拉应力;y为负时,σ为压应力。一点的应力是拉应力或压应力,也可由弯曲变形直接判定,不一定借助于坐标y的正负。因为,以中性层为界,梁在凸出的一侧受拉。这样,就可把y看作一点到中性轴的距离的绝对值。

导出式(9-9)和式(9-10)时,为了方便,我们是把梁截面画成矩形的。但在推导过程中,并未用到矩形的任何几何特性。所以,只要梁有一纵向对称面,且载荷作用于这个平面内,此两式就适用。

例9-1　图9-4(a)所示的矩形截面悬臂梁承受均布载荷q作用。已知q=10N/mm,l=300mm,b=20mm,h=30mm。试求截面B上C、D两点的正应力。

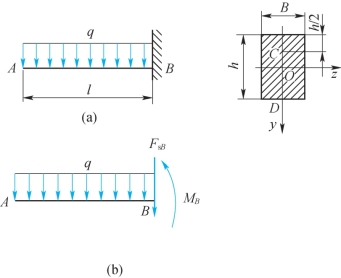
图9-4

解:(1)求截面B上的弯矩。

AB受力分析如图9-4(b)所示,由截面法,得

(2)求截面B上C、D处的正应力。

由式(9-10),有

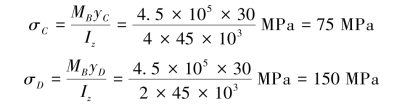
因截面B上的弯矩为负,故横截面中性轴z以上各点产生拉应力、中性轴z以下各点产生压应力。所以,点C处为拉应力,点D处为压应力。

思政提示

弯曲梁横截面以中心轴为界,分为拉伸部分和压缩部分,两个部分相互影响,对立统一。这就像一个团体,要有活力和创新力,其内部就必须有竞争(对立),但又必须保持一定的约束(统一)。对立和统一缺一不可,只有平衡好这两方面的关系,这个团体才会发展得快,才能取得成功。