观察图8-11,因该梁的载荷特征,其内力方程需分两段列出,即其内力方程共有4个。对于这种内力方程较多的梁,依据内力方程作剪力图与弯矩图,则是项较烦琐的工作。因此,我们试图分析剪力、弯矩与载荷集度之间是否存在某种数学关系,以便据此找到剪力图、弯矩图的某些规律,从而快速、简便地作图。

图8-12(a)所示的梁受分布载荷q=q(x)作用。为了寻找剪力、弯矩沿梁轴的变化情况,选梁的左端为坐标原点,用距离原点分别为x、x+dx的两个横截面m—m、n—n从梁中切取一微段进行分析,其受力如图8-12(b)所示。

图8-12

设微段的m—m截面上的内力为Fs、M,n—n截面上的内力则应为Fs+dFs、M+dM。此外,微段上还作用着分布载荷(dx上作用的分布载荷可视为均布)。

由平衡方程

得

由平衡方程

∑MC(F)=M+dM-qdx·-Fsdx-M=0(略去其中的高阶微量qdx·

得

由式(8-1)、式(8-2)得

式(8-1)　～式(8-3)即为剪力、弯矩与载荷集度之间的微分关系式。

依据上面所推出的Fs、M、q之间的微分关系,我们可以总结出在几种载荷作用下剪力图、弯矩图的固有规律、特征(见表8-2),以帮助我们快速作出弯矩图(M图)、内力图(Fs图)。

表8-2

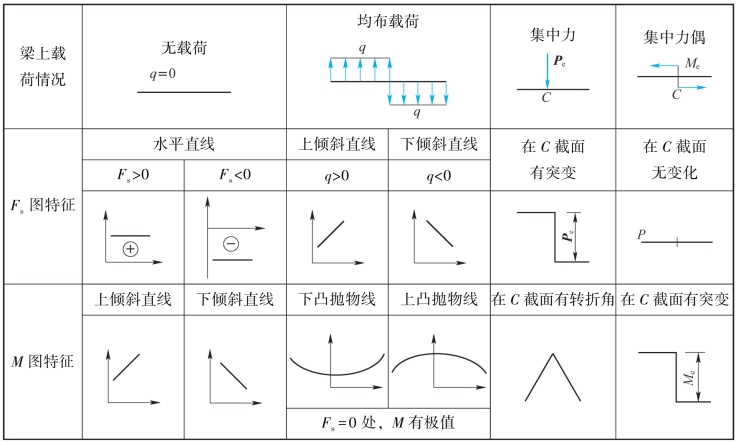
(1)若梁上某一段无分布载荷作用,即q(x)=0,由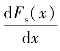=q(x)=0可以知道,在这段梁内剪力Fs为常数,即剪力图为平行于x轴的水平直线,如图8-11(b)中梁CA段的剪力图。这时,由=常数,可以知道该梁段的弯矩图必为斜直线,如图8-11(c)中梁CA段因剪力为负常数-20kN,所以其弯矩图为下斜直线。当某段梁剪力为0时,其弯矩图必为水平直线。

(2)若梁上某一段内作用均布载荷,即有q(x)=常数。由=q=常数可以知道,这段梁的剪力图必为斜直线。由于剪力方程为x的线性函数,因此弯矩方程M(x)必为二次函数,即弯矩图为抛物线。这时,弯矩图的凹凸方向由=q,即均布载荷q的正负符号确定。如图8-11(a)中的梁AB段,q=-10kN/m＜0,其剪力图为下斜直线,如图8-11(b)所示,弯矩图为上凸抛物线,如图8-11(c)所示。反之,q＞0时,剪力图为上斜直线,弯矩图为下凸抛物线。

(3)在集中力作用处,剪力图发生突变,其突变的数值等于该集中力的大小,如图8-11(b)中的截面A剪力突变了35kN,恰为该截面上支反力的数值。同时,由于该截面处剪力突变,弯矩图的斜率也发生突变,成为一个转折点。在集中力偶作用处,弯矩图发生突变,突变的数值等于该集中力偶矩的大小,如图8-11(c)中截面A的弯矩突变了40N·m,恰等于梁上该截面处的外力偶矩的数值。

从上面的分析可以知道,凡是集中力或集中力偶作用的截面上,剪力图或弯矩图都发生突变,剪力或弯矩似乎没有确定的数值。

事实上,所谓集中力并不可能完全“集中”作用于一点,它是分布于一个微段Δx内的分布力经简化后得到的结果,如图8-13(a)所示。若在Δx范围内把载荷看成是均匀分布的,则剪力连续地从Fs1变化到Fs2,如图8-13(b)所示。关于集中力偶作用的截面上弯矩数值的突变,也可作同样的解释。

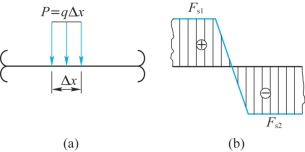
图8-13

(4)若在梁的某一截面上剪力Fs=0,即=0,说明弯矩图在该截面处的斜率为0,则该截面处的弯矩就是梁在这段内的极值。如图8-11(c)所示,在x=2.5m处的截面上,Fs=0,其弯矩M=31.25kN·m,即为梁AB段内弯矩的极值。同时,这个极值弯矩也是整个梁上弯矩的最大值,即有Mmax=31.25kN·m。有时,Mmax也可能发生在集中力或集中力偶的作用处。因此,在求梁上的|M|max时,应综合考虑上述的各种可能性。

例8-4　图8-14所示的外伸梁,受集中力F=10kN,均布载荷集度q=10N/cm作用,图中长度单位为m,试利用剪力、弯矩与载荷集度的微分关系绘制出梁的剪力图、弯矩图。

分析:(1)对此外伸梁,在求内力前,只需求出点A的支反力。　(2)梁上A、C、D 3点处作用着集中力(A、D两点处作用着支座约束反力),故剪力在这3点处发生突变,而该处的弯矩无突变。(3)AC、CD两段上没有均布载荷作用(q=0),故该两段梁的剪力图为水平直线,只需用截面法分别求出AC、CD段上某一个截面的剪力即可画出两段梁的剪力图。而AC、CD两段梁的弯矩图为斜直线,需确定两个点,所以用截面法分别求出两段梁上某两个截面的弯矩。(4)BD段上有均布载荷作用(q＜0),故该段剪力图为一斜直线,需求出BD段上某两个截面上的剪力。而BD段的弯矩图为一上凸的抛物线,所以,首先需求出B、D截面的弯矩,再根据Fs=0处,M有极值,来确定抛物线的极值点。

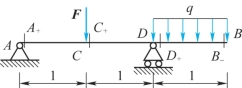
图8-14

解:

(1)求A处约束力。

由∑MA(F)=R·2-F·1+q·=0,得R=4.75kN。

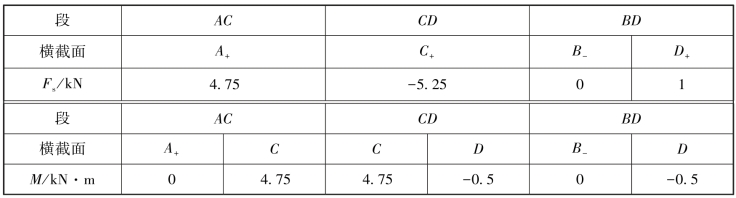
(2)用截面法,求各段梁关键截面的内力,列表计算,如表8-3所示。

表8-3

(3)由关键点画剪力图与弯矩图,如图8-15所示。

例8-5　图8-16(a)所示的悬臂梁,在其BC段作用有均布载荷q,自由端作用一个P=qa/2的集中力,试作梁的剪力图与弯矩图。

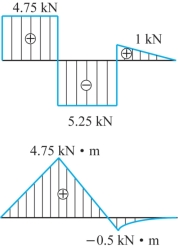
图8-15

(www.daowen.com)

图8-16

分析:(1)此梁为悬臂梁,可以不求约束力。　(2)根据该梁受力特点,内力图需分AB、BC两段考虑。(3)AB段上无均布载荷作用,剪力图为水平直线,弯矩图为斜直线,我们可以选A+、B为关键点,用截面法分别求出A+截面的剪力、弯矩及B截面的弯矩。(4)BC段有向下作用的均布载荷,其剪力图为斜直线,弯矩图为上凸的抛物线。我们需求出B、C两截面的剪力及弯矩,并确定该段上剪力为0之点所在位置,以此确定弯矩极值点所在位置,并求出弯矩的极值。

解:(1)用截面法计算AB、BC段关键截面的剪力、弯矩值,列表计算,如表8-4所示。

表8-4

续表

(2)画剪力图、弯矩图,如图8-16(b)、(c)所示。

思政提示

利用载荷集度、剪力和弯矩间的关系绘制剪力图和弯矩图,能显著提高作图效率。做其他工作也一样,找到各事物间的内在联系,发现规律、利用规律,能达到事半功倍的效果,这就是所谓的磨刀不误砍柴工。

习　题

8-1　利用截面法求如题8-1图所示各梁中截面1—1、2—2和3—3上的剪力和弯矩,图中长度单位为mm。这些截面无限接近于截面C或截面D。设P、q、a均为已知。

题8-1图

8-2　绘制如题8-2图所示各梁的剪力图和弯矩图,并求出

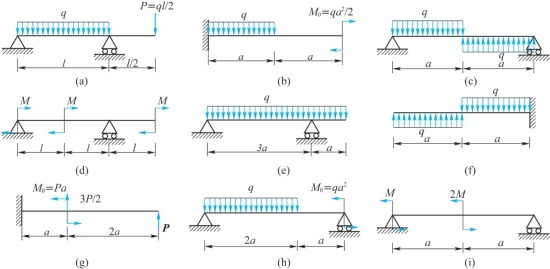
题8-2图

8-3　利用梁的内力微分关系对题8-2图中的内力图进行校核。

8-4　试作如题8-4图所示多跨静定梁的剪力图和弯矩图,图中长度单位为m。

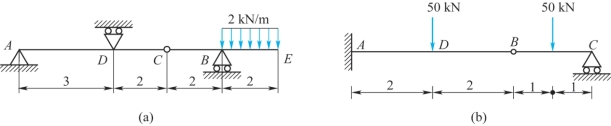
题8-4图

8-5　如题8-5图所示,起重机大梁上的小车的每个轮子对大梁的压力均为P,试问小车在什么位置时梁内弯矩为最大?其最大弯矩等于多少?设小车的轮距为d,大梁的跨度为l。

8-6　如题8-6图所示,起吊一根自重为q(N/m)的等截面钢筋混凝土杆,问吊装时起吊点位置x应为多少才最合理(最不容易使杆折断)?

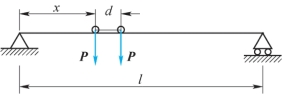
题8-5图

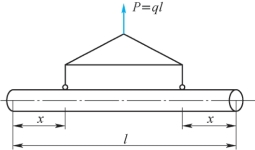
题8-6图

8-7　根据梁的载荷集度q、剪力Fs和弯矩M间的微分关系,改正如题8-7图所示剪力图和弯矩图的错误。

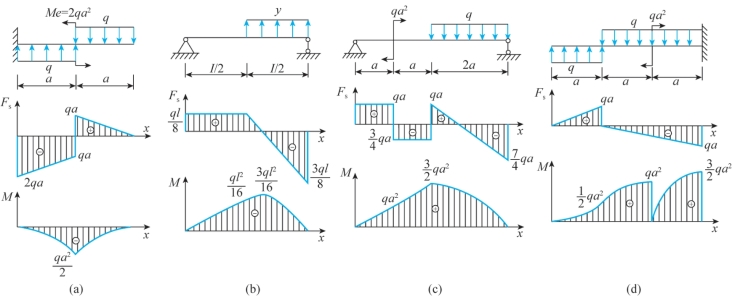
题8-7图

8-8　设梁的剪力图或弯矩图如题8-8图所示,试补充这些梁所缺的弯矩图、剪力图和载荷图,图中长度单位为m。已知梁上没有集中力偶作用。

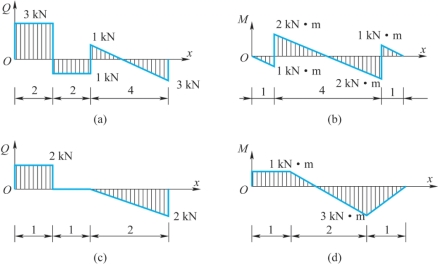
题8-8图

8-9　如题8-9图所示,作梁ABC的剪力图和弯矩图。

8-10　梁的剪力图如题8-10图所示,作弯矩图及载荷图。已知梁上没有作用集中力偶。

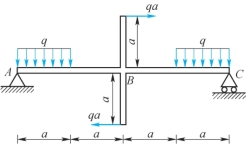
题8-9图

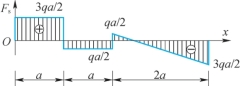
题8-10图

8-11　作如题8-11图所示刚架的弯矩图。

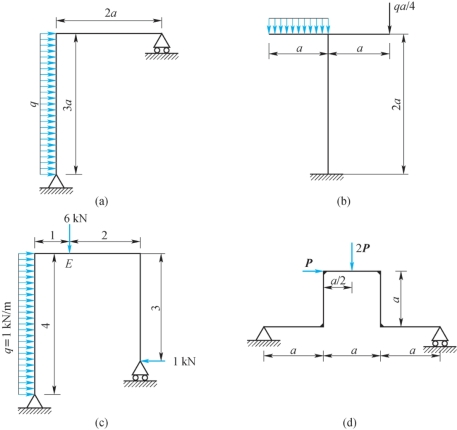
题8-11图