梁的强度和刚度分析在材料力学中占有重要的地位;而梁的内力分析对解决梁的承载能力非常关键。如图8-7(a)所示的任意梁,其所受外力均为已知,现在研究其任一横截面m—m上的内力(该横截面离梁左端的距离为b)。

图8-7

如图8-7(b)所示,利用截面法,在截面m—m处将梁假想地切开,并任选一段(如左段)作为研究对象。为了分析内力,将左段梁上的所有外力均向截面m—m的形心C简化,得主矢Fs′与主矩M′。由于外力均垂直于梁轴,因此主矢量Fs′也垂直于梁轴。由此可见,当梁弯曲时,横截面上必然同时存在两种内力分量:与主矢Fs′平衡的内力Fs;与主矩M′平衡的内力偶矩M。内力Fs即前述剪力;矢量位于所切横截面的内力偶矩M,即前述弯矩。

根据左段梁的平衡条件,由平衡方程

∑Fy=0,FAy-F1-Fs=0

得

Fs=FAy-F1

即剪力等于左段梁上所有外力的代数和。

由平衡方程

∑MC(F)=0,M+F1(b-a)-FAyb=0

得

M=FAy-F1(b-a)

即弯矩等于左段梁上所有外力对形心C的力矩的代数和。

截面m—m上的剪力与弯矩,也可利用切开后的右段梁的平衡条件求得。

关于剪力与弯矩的正负符号,规定如下:在所切横截面的内侧切取微段,如图8-8(a)所示,凡企图使微段沿顺时针方向转动的剪力为正,使微段下边受拉、上边受压的弯矩为正,如图8-8(b)所示。按此规定,图8-7(b)中剪力与弯矩均为正。

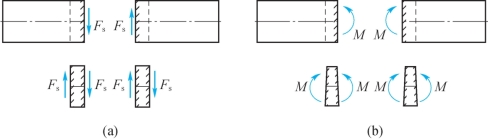
图8-8

综上所述,可将计算剪力与弯矩的方法概括如下:

(1)在需求内力的横截面处,假想地将梁切开,并选切开后的任一段为研究对象;

(2)画所选梁段的受力图,图中剪力Fs与弯矩M可假设为正;

(3)由平衡方程∑Fy=0计算剪力Fs;

(4)由平衡方程∑MC=0计算弯矩M,C为所切横截面的形心。

例8-1　如图8-9(a)所示,外伸梁承受集中力F与矩为Me=Fl的集中力偶作用,试计算横截面E、横截面A+与D-的剪力与弯矩。截面A+代表距横截面A无限近并位于其右侧的截面;D-代表距横截面D无限近并位于其左侧的横截面。

解:(1)计算支反力。

设支座A与B处的铅垂支反力分别为FAy与FBy,则由平衡方程

∑MA(F)=0,FByl-F·2l-Fl=0

∑Fy(F)=0,FBy-FAy-F=0

得

FAy=2F,FBy=3F

在横向力与力偶作用下的静定梁,固定铰支座处的水平支反力必为0。因此,在画梁的受力图时,固定铰支座处的水平支反力一般可省略不画。

图8-9

(2)计算截面E的剪力与弯矩。

在截面E处假想地将梁切开,并选左段为研究对象,如图8-9(b)所示。由平衡方程∑Fy=0与∑MC(F)=0(C为截面E的形心),得截面E的剪力与弯矩分别为

(3)计算截面A+的剪力与弯矩。

在截面A+处假想地将梁切开,并选左段为研究对象,如图8-9(c)所示,由平衡方程∑Fy=0得截面A+的剪力为

由平衡方程∑MC1(F)=0(C1为截面A+的形心),得该截面的弯矩为

(4)计算截面D-的剪力与弯矩。

在截面处假想地将梁切开,并为计算简单,选择切开后的右段为研究对象,如图8-9(d)所示,由平衡方程∑Fy=0与∑MC2(F)=0,得

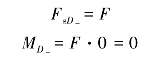
通过弯曲内力的分析可以看出,在一般情况下,梁的横截面上的剪力和弯矩是随横截面的位置变化而变化的。

1)剪力方程与弯矩方程

将构件各横截面上的剪力、弯矩表示为坐标位置x的函数,即

Fs=Fs(x)(www.daowen.com)

M=M(x)

其表示的剪力、弯矩随截面位置而变化的函数关系分别称为剪力方程和弯矩方程。在建立剪力方程和弯矩方程时,一般是以梁的左端为坐标原点。有时,为了方便计算,也可将坐标原点取在梁的右端或其他位置。

2)剪力图与弯矩图

在实际工程中,为了简明而直观地表明梁的各截面上剪力Fs和弯矩M的大小变化情况,需要绘制剪力图和弯矩图。可仿照轴力图或扭矩图的作法,以截面沿梁轴线的位置为横坐标x,以截面上的剪力Fs或弯矩M数值为对应的纵坐标,选定比例尺绘制剪力图和弯矩图。对水平梁,绘图时将正值的剪力画在x轴的上方;至于正值的弯矩,则画在梁的受压一侧,即x轴的上方。

由剪力方程和弯矩方程,特别是剪力图和弯矩图,可以确定梁的剪力和弯矩的最大值,以及剪力和弯矩为最大值的截面,这些截面称为危险截面。剪力方程和弯矩方程,以及剪力图和弯矩图是梁的强度计算和刚度计算的重要依据。

例8-2　图8-10(a)为简支梁是齿轮传动轴的计算简图。试列出它的剪力方程和弯矩方程,并作剪力图和弯矩图。

图8-10

解:由静力平衡方程

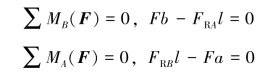
得支座约束反力为

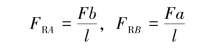
以梁的左端为坐标原点,选取坐标系如图8-10(a)所示。集中力F作用于点C,梁在AC和CB两段内的剪力或弯矩不能用同一方程式来表示,应分段考虑。在AC段内取距原点为x的任意截面,截面以左只有外力FRA,根据剪力和弯矩的计算方法和符号规则,求得这一截面上的Fs和M分别为

这就是在AC段内的剪力方程和弯矩方程。如在CB段内取距左端为x的任意截面,则截面以左有FRA和F两个外力,截面上的剪力和弯矩是

当然,如用截面右侧的外力来计算会得到相同的结果。

由式(a)可知,在AC段内梁的任意横截面上的剪力皆为常数Fb/l,且符号为正,所以在AC段(0＜x＜a)内,剪力图是在x轴上方且平行于x轴的直线,如图8-10(b)所示。同理,可以根据式(c)作CB段的剪力图。从剪力图看出,当a＜b时,最大剪力为=Fb/l。

由式(b)可知,在AC段内弯矩是x的一次函数,所以弯矩图是一条斜直线。只要确定线上的两点,就可以确定这条直线。例如,x=0处,M=0;x=a处,M=Fab/l。连接这两点就得到AC段内的弯矩图,如图8-10(c)所示。同理,可以根据式(d)作CB段内的弯矩图。从弯矩图看出,最大弯矩在截面C上,且Mmax=Fab/l。

例8-3　绘制图8-11(a)所示外伸梁CAB的剪力图和弯矩图,图中长度单位为m。

图8-11

解:(1)求梁的支反力。

根据图8-11(a)所示梁的受力图列出其平衡方程

得支反力

FA=35kN,FB=25kN

利用∑Fy=0校核,说明支反力的计算是正确的。

(2)写出梁的剪力方程和弯矩方程。

根据该梁的受力情况可知,内力函数在CA段和AB段的表达式不同。选取如图8-11(a)所示的坐标系,CA段梁的剪力方程和弯矩方程分别为

AB段梁的剪力方程和弯矩方程分别为

(3)确定绘制内力图控制截面的内力数值。

剪力Fs1和Fs2及弯矩M1的方程均为线性函数,其图形为直线,只需确定这些图线端点的内力数值。而弯矩M2的方程为二次函数,只有确定较多的点才能画出该抛物线。根据梁的强度和刚度分析的需要,内力数值最大的点要准确地在内力图上确定。为了确定梁段AB内弯矩为极值的截面位置,令

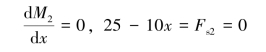
即梁AB段内弯矩为极值的截面在剪力为0处,其位置x0为

x0=2.5m

将其代入弯矩M2的方程,可求出AB梁段内的极值弯矩为

列出梁的内力图的控制截面的内力数值,如表8-1所示。

表8-1

(4)作梁CAB的剪力图和弯矩图,如图8-11(b)和图8-11(c)所示,从图中可以明显地看出

思政提示

求梁的剪力方程和弯矩方程进而画剪力图和弯矩图是一项烦琐且易出错的工作。对于这样的工作,我们要保持认真负责、踏实敬业的工作态度和严谨求实、一丝不苟的职业素养。