如前所述,轴的扭转变形用横截面间绕轴线的相对角位移即扭转角φ表示。

由式可知,微段dx的扭转变形为

因此,相距l的两横截面间的扭转角为

由此可见,对于长为l、扭矩T及切变模量G均为常数的等截面圆轴,其两端横截面间的相对转角即扭转角为

上式表明,扭转角φ与扭矩T、轴长l成正比,与GIp成反比。GIp称为圆轴截面的扭转刚度,或简称为扭转刚度。

例7-3　如图7-21(a)所示,有A、B两个凸缘的圆轴在扭转力偶矩Me作用下发生了变形。这时,把一个薄壁圆筒与轴的凸缘焊接在一起,然后解除Me,如图7-21(b)所示。设轴和筒的扭转刚度分别是G1Ip1和G2Ip2,试求轴和筒分别承受的扭矩。

解:由于筒与轴的凸缘焊接在一起,因此外加扭转力偶矩Me解除后,圆轴必然力图恢复并消除扭转变形,而圆筒则阻挡其恢复,这就使得在轴内和筒内分别出现扭矩T1和T2。设想用横截面把轴与筒切开,因这时已无外力偶矩,所以平衡方程是

(www.daowen.com)

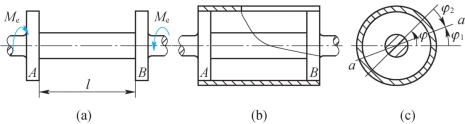
图7-21

仅由式(a)不能解出两个扭矩,所以这是一个超静定问题,应再寻求一个变形协调方程。

焊接前轴在扭转力偶矩作用下的扭转角为

这就是凸缘B的水平直径相对于A转过的角度,如图7-21(c)所示。在筒与轴相焊接并解除Me后,因受筒的阻挡,轴的上述变形不能完全恢复,最后协调的位置为a—a。这时,圆轴残留的扭转角为φ1,而圆筒产生的扭转角为φ2。显然

φ1+φ2=φ

利用式(7-25)和式(b),可将上式写成

由式(a)、式(c)解出