1)切应力互等定理

在小变形的前提下,圆轴扭转时横截面始终保持为平面,而且形状、大小不变,半径仍为直线,截面之间的距离也不变。所以,在横截面上没有正应力,而切应力与过这点的半径垂直,朝向与截面上的扭矩转向相一致。在图7-12(a)所示的纯扭转圆轴中取一个微体,它的边长分别是dx、dy和δ,如图7-12(b)所示。

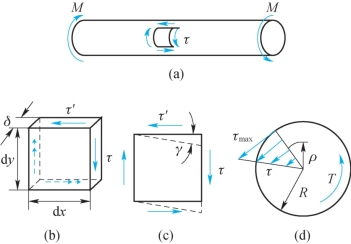
图7-12

在微体的左右侧面各有一个相等的剪力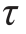δdy,它们的方向相反,组成一个力偶,其力偶矩是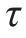δdydx。因为微体处于平衡状态,所以在微体的顶面和底面必定存在切应力,上下两个面的剪力必然也组成一个反力偶,反力偶矩是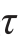′δdxdy,与上述的力偶相平衡,即

所以

可见,微体的两个正交面上如果有切应力的话,则切应力的数值相等,方向与两个正交面的交线垂直,共同指向或共同背离交线。这就是切应力互等定理。上面微体的4个侧面只有切应力没有正应力,这种应力状态称为纯剪切。

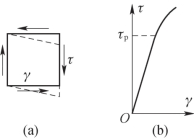
图7-13

2)剪切胡克定律

在切应力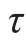作用下,微体发生切应变γ,如图7-13(a)所示。薄壁圆管的扭转试验表明,当切应力不超过材料的剪切比例极限p时,切应力与切应变成正比,如图7-13(b)所示,即

引进比例系数G,则

式(7-8)称为剪切胡克定律。比例系数G称为切变模量,其值随材料而异,并由试验测定。例如,钢的切变模量G=75～80GPa,铝与铝合金的切变模量G=26～30GPa。

还应指出,理论与试验研究均表明,对于各向同性材料,弹性模量E、泊松比μ与切变模量G之间存在如下关系

因此,当已知任意两个弹性常数后,由上述关系可以确定第三个弹性常数。由此可见,各向同性材料只有两个独立的弹性常数。

图7-14

3)扭转的切应力公式与极惯性矩和抗扭截面的计算

在获得了圆截面上的切应力分布后,现在来分析切应力与扭矩之间的关系。

如图7-14所示,在半径为ρ的圆周处取一个微面积dA,上面作用微剪力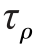dA,它对圆心O的微力矩是ρdA,所有这些微力矩的和等于截面上的扭矩,即

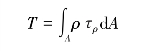
将公式代入上式得

令上式中的积分为Ip,它仅与截面的几何尺寸有关,称为极惯性矩,即

(www.daowen.com)

由此可以得到

把式(7-12)代入式(7-6)中,并联立式(7-8)就得到切应力计算公式

显然,横截面上的最大切应力为

式中,Ip/R项也是一个仅与截面有关的量,称为抗扭截面系数,用Wt表示,即

所以,最大切应力计算公式又可以写成

4)极惯性矩和抗扭截面系数的计算

直接用积分就可以求出圆截面的极惯性矩和抗扭截面系数。

如图7-15所示,取微面积dA=ρdθdρ,代入式Ip=dA中,得到极惯性矩,即

把式(7-17)代入式Wt=中得到抗扭截面系数

如图7-16所示,如果是空心圆截面,用相同的的方法可以求出极惯性矩和抗扭截面系数

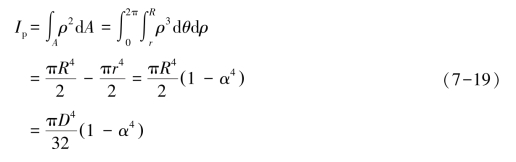
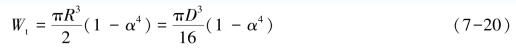
其中,α是内径与外径之比,即

空心圆截面上的切应力分布如图7-17所示。

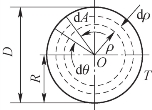
图7-15

图7-16

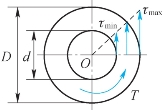
图7-17

思政提示

切应力互等定理也称之为切应力双生定理,切应力在相邻的两个面上是成对出现、和谐共生的。“万物各得其和以生,各得其养以成”,我们要树立社会主义生态文明观,推动形成人与自然和谐发展现代化建设新格局。