1)纯扭转

如图7-11(a)所示,一根等截面圆轴,两端受到一对力偶作用,轴内扭矩是一常量,此时圆轴所发生的扭转变形称为纯扭转。在小变形的条件下,由对称性知,轴的横截面在绕轴线转动的过程中仍保持为平面,它的形状还是圆,半径仍是直线,轴的长度和半径的大小都保持不变。左右两端截面绕轴线相对转过一个角度φ,称为扭转角。假设左端面转过的角度是0,则右端面转过角度就是φ,轴内任一横截面的扭转角用φ(x)表示。

2)切应变和扭曲率

在纯扭转的圆轴内用两个横截面截出长度为dx的微段,如图7-7(b)所示。两截面绕轴线相对转过的角度是dφ,两条母线ad和bc分别倾斜了一个相同的角度。矩形abcd变形成平行四边形abc′d′,ab与ad的夹角由90°减小了一个角度γmax,这个角度的改变称为切应变。在小变形的条件下,由图示的几何关系得到

式中,dφ/dx表示单位长度上的扭转角,或者表示扭转角沿着轴线的变化率,称为扭曲率,用符号θ表示,即

在纯扭转的情况下,扭曲率可以用轴两端截面的扭转角φ除以轴的长度l来表示,即(www.daowen.com)

由此可以得到圆轴外表面的切应变的表达式

根据类似的分析可以得到圆轴内部的切应变,如图7-11(c)所示。在dx的微段内截出半径为ρ的圆柱体,因为半径仍保持直线,所以其表面的切应变为

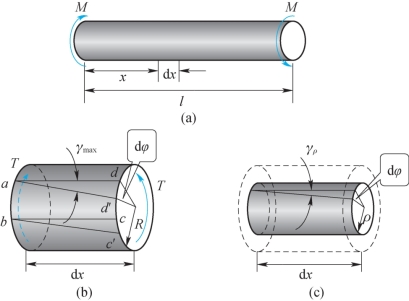
图7-11