在工程中,常用铆钉、螺栓、键或销钉等将构件相互连接,这些起连接作用的部件统称为连接件。连接件的受力与变形一般是很复杂的,很难进行精确的理论分析。因此,工程中通常采用实用的简化分析方法或称为假定计算方法。其要点是:一方面,假定应力分布规律,从而计算出各部分的“名义应力”;另一方面,根据实物或模拟试验,并采用同样的计算方法,由破坏载荷确定材料的极限应力,然后再根据上述两方面的结果建立其强度条件。

实践表明,这种假定计算方法是可靠的。现以铆钉连接为例,介绍有关概念与计算方法。

考察图6-31(a)所示的铆钉连接,显然,铆钉在两侧面上分别受到大小相等、方向相反、作用线相距很近的两组外力系的作用,如图6-31(b)所示。铆钉在这样的外力作用下,将沿两侧外力之间,并与外力作用线平行的截面m—m发生相对错动,这种变形形式称为剪切。发生剪切变形的截面m—m,称为受剪面或剪切面。应用截面法,可求得受剪面m—m上的剪力Fs,如图6-31(c)所示。在实际工程计算中,通常假定受剪面上的切应力均匀分布,于是,受剪面上的名义切应力为

式中,Fs为受剪面上的剪力;As为受剪面的面积。

图6-31

然后,通过直接试验,并按式(6-28)求得剪切破坏时材料的极限名义切应力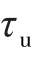,再除以安全因数,即得材料的许用切应力[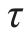]。于是,剪切强度条件为

需要注意,在计算中要正确确定有几个受剪面,以及每个受剪面上的剪力。

思政提示

杆件的连接部分往往同时受到剪切和挤压作用,如果忽视了其中某一项便进行校核和计算,容易导致杆件失效。在生活中,与他人的交流和沟通也值得引起充分的重视。如果沟通不畅,往往会导致产生误会和误解,轻则影响人际关系,重则导致工作难以开展。应当注意沟通的方式和方法,注意聆听对方的需求和意见,在真诚的交流和沟通中,协调团队关系,促进团队合作,顺利达成目标。

习　题

6-1　拉杆或压杆如题6-1图所示。试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。

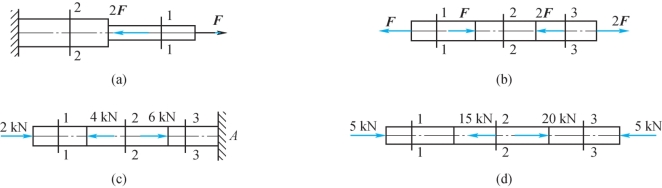
题6-1图

6-2　圆截面钢杆长l=3m,直径d=25mm,两端受到F=100kN的轴向拉力作用时伸长量Δl=2.5mm。试计算钢杆横截面上的正应力σ和轴向线应变ε。

6-3　阶梯状直杆受力如题6-3图所示。已知AD段横截面面积AAD=1000mm2,DB段横截面面积ADB=500mm2,材料的弹性模量E=200GPa。求该杆的总变形量ΔlAB。

6-4　圆截面阶梯状杆件如题6-4图所示,受到F=150kN的轴向拉力作用。已知中间部分的直径d1=30mm,两端部分直径d2=50mm,整个杆件的长度l=250mm,中间部分杆件的长度l1=150mm,弹性模量E=200GPa。试求:　(1)各部分横截面上的正应力σ;(2)整个杆件的总伸长量。

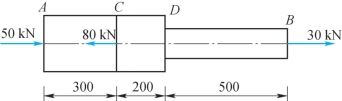
题6-3图

题6-4图

6-5　用一根灰口铸铁圆管作受压杆。已知材料的许用应力[σ]=200MPa,轴向压力F=1000kN,管的外径D=130mm,内径d=30mm。试校核其强度。

6-6　如题6-6图所示,用绳索吊起重物。已知F=20kN,绳索横截面面积A=12.6cm2,许用应力[σ]=10MPa。试校核α=45°及α=60°两种情况下绳索的强度。

6-7　某悬臂吊车如题6-7图所示。最大起重载荷G=20kN,杆BC为Q235A圆钢,许用应力[σ]=120MPa,图中长度单位为m。试按图示位置设计杆BC的直径d。

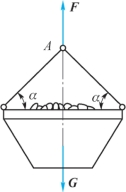
题6-6图

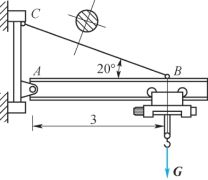
题6-7图(www.daowen.com)

6-8　如题6-8图所示,杆AC、BC铰接于C,并吊起重力为G的重物。已知杆BC许用应力[σ1]=160MPa,杆AC许用应力[σ2]=100MPa,两杆横截面面积均为A=2cm2。求所吊重物的最大质量。

6-9　三角架结构如题6-9图所示,图中长度单位为m。已知杆AB为钢杆,其横截面面积A1=600mm2,许用应力[σ1]=140MPa;杆BC为木杆,横截面面积A2=3×104mm2,许用应力[σ2]=3.5MPa。试求许用载荷[F]。

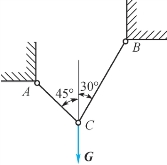
题6-8图

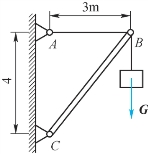
题6-9图

6-10　一板状试样如题6-10图所示,表面贴上纵向和横向电阻应变片来测定试样的应变。已知b=4mm,h=30mm,每增加ΔF=3kN的拉力,测得试样的轴向线应变变化量Δε=120×10-6,径向线应变变化量Δε′=-38×10-6。试求材料的弹性模量E和泊松比μ。

6-11　如题6-11图所示,正方形截面阶梯状杆件的上段是铝制杆,边长a1=20mm,材料的许用应力[σ1]=80MPa;下段为钢制杆,边长a2=10mm,材料的许用应力[σ2]=140MPa,图中长度单位为m。试求许用载荷[F]。

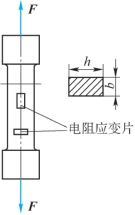
题6-10图

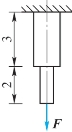
题6-11图

6-12　两端固定的等截面直杆受力如题6-12图所示,求两端的支座反力。

6-13　如题6-13图所示,切料装置用刀刃把切料模中φ12mm的棒料切断。棒料的抗剪强度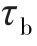=320MPa。试计算切断力。

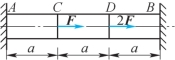
题6-12图

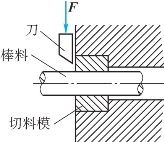
题6-13图

6-14　题6-14图所示螺栓受拉力F作用。已知材料的许用切应力[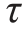]和许用拉应力[σ]的关系为[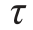]=0.6[σ]。试求螺栓直径d与螺栓头高度h的合理比例。

6-15　已知螺栓的许用切应力[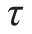]=100MPa,钢板的许用拉应力[σ]=160MPa。试计算题6-15图所示焊接板的许用载荷[F]。

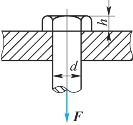
题6-14图

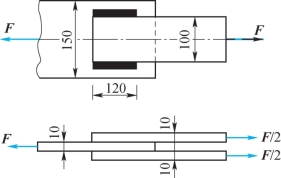
题6-15图

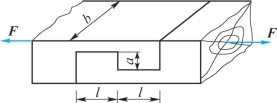
6-16　矩形截面的木拉杆的接头如题6-16图所示。已知轴向拉力F=50kN,截面宽度b=250mm,木材的顺纹许用挤压应力[σbs]=10MPa,顺纹许用切应力[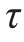]=1MPa。求接头处所需的尺寸l和a。

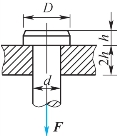
6-17　题6-17图所示连接构件中D=2d=32mm,h=12mm,拉杆材料的许用应力[σ]=120MPa,[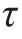]=70MPa,[σbs]=170MPa。试求拉杆的许用载荷[F]。

题6-16图

题6-17图