绝对变形的大小只反映杆件的总变形量,而无法说明杆件的变形程度。因此,为了度量杆件的变形程度,还需计算单位长度内的变形量。对于轴力为常量的等截面直杆,其变形处处相等。可将Δl除以l,Δd除以d表示单位长度的变形量,即

式中,ε称为轴向线应变;ε′称为径向线应变。应变是单位长度的变形,是无因次的量。由于Δl与Δd具有相反符号,因此ε与ε′也具有相反的符号。将式(6-15)代入式(6-17),得胡克定律的另一表达形式为

显然,式(6-19)中的轴向线应变ε和横截面上正应力的正负号也是相对应的。式(6-19)是经过改写后的胡克定律,它不仅适用于拉压杆,而且更普遍地适用于所有的单轴应力状态,故通常又称为单轴应力状态下的胡克定律。

试验表明,当拉压杆内应力不超过某一限度时,径向线应变ε′与轴向线应变ε之比的绝对值为一常数,即

μ称为径向变形因数或泊松比,是无因次的量,其数值随材料而异,也是通过试验测定的。

弹性模量E和泊松比μ都是材料的弹性常数。

必须指出,当杆件沿轴向为非均匀变形时,式(6-17)并不反映其沿轴向各点处的轴向线应变。如图6-13所示,对于各处变形不均匀的情形,则必须考虑杆件上沿轴向的微段dx的变形,并以微段dx的相对变形来度量杆件局部的变形程度,A(x)为微段面积。这时有

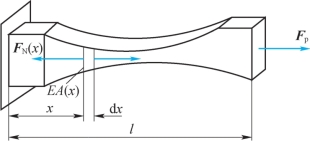
图6-13

可见,无论变形均匀还是不均匀,正应力与正应变之间的关系都是相同的。(www.daowen.com)

例6-5　已知阶梯形直杆受力如图6-14(a)所示,图中长度单位为mm,材料的弹性模量E=200GPa,杆件各段的横截面面积分别为AAB=ABC=1500mm2,ACD=1000mm2。要求:(1)画轴力图;(2)计算杆的总伸长量。

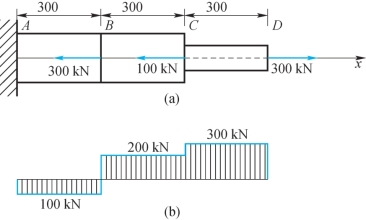
图6-14

解:

(1)画轴力图。因为在A、B、C、D处都有集中力作用,所以杆AB、BC和CD的轴力各不相同。应用截面法得

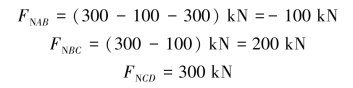
轴力图如图6-14(b)所示。

(2)求杆件的总伸长量。因为杆件各段轴力不等,且横截面面积也不完全相同,所以必须分段计算各段的变形,然后求和。杆件各段的轴向变形分别为

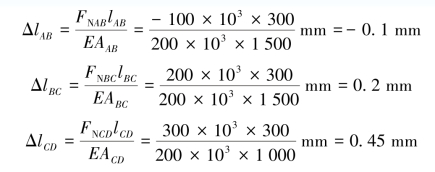
杆件的总伸长量为

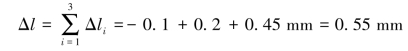
思政提示

杆件的变形量与杆件材料的弾性模量相关,弹性模量越大,杆件变形量越小。人也是这样,内心越强大时,就越能顶住外界压力,做好自己的工作;反之,内心不够强大时,就容易受到外界因素影响,从而失去自己的主意和原则,随波逐流。