前文研究了拉压杆横截面上的应力,为了更全面地了解杆内的应力情况,下面研究斜截面上的应力。如图6-7(a)所示拉杆,利用截面法,沿任一斜截面m—m将杆件截开,取左段杆为研究对象,该截面的方位以其外法线On与x轴的夹角α表示。由平衡条件可得斜截面m—m上的内力为

由前述分析可知,杆件横截面上的应力均匀分布,由此可以推断,斜截面m—m上的总应力pα也为均匀分布,且其方向必与杆轴平行,如图6-7(b)所示。设斜截面的面积为Aα,Aα与横截面面积A的关系为Aα=A/cosα。于是

式中,σ0=为拉杆在横截面(α=0°)上的正应力。

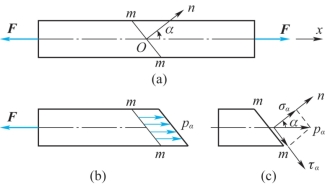
图6-7

如图6-7(c)所示,将总应力pα沿截面法向与切向分解,得斜截面上的正应力与切应力分别为

上列两式表示通过拉压杆内任一点处不同方位截面上的正应力σα和切应力随截面方位角α的变化而变化。通过一点的所有不同方位截面上的应力的集合,称为该点处的应力状态。由式(6-6)、式(6-7)可知,在所研究的拉杆中,任一点处的应力状态由其横截面上的正应力σ0即可完全确定,这样的应力状态称为单轴应力状态。关于应力状态的问题将在第11章中详细讨论。

由式(6-6)、式(6-7)可知,通过拉压杆内任一点不同方位截面上的正应力σα和切应力,随α角作周期性变化。

(1)当α=0°时,正应力最大,即

说明拉压杆的最大正应力发生在横截面上。

(2)当α=45°时,切应力最大,即

说明拉压杆的最大切应力发生在与杆轴线成45°的斜截面上。

为便于应用上述公式,现对方位角与切应力的正负号作如下规定:以x轴为始边,方位角α为逆时针转向者为正;斜截面外法线On沿顺时针方向旋转90°,与该方向同向的切应力为正。按此规定,图6-7(c)中的α与均为正。

当等直杆受几个轴向外力作用时,由轴力图可求得其最大轴力FN,max,那么杆内的最大正应力为

最大轴力所在的横截面称为危险截面,危险截面上的正应力称为最大工作应力。

例6-2　一正方形截面的阶梯形砖柱,其受力情况、各段长度及横截面尺寸如图6-8(a)所示。已知P=40kN,试求载荷引起的最大工作应力。

解:首先作柱的轴力图,如图6-8(b)所示。由于此柱为变截面杆,因此应分别求出每段柱的横截面上的正应力,从而确定全柱的最大工作应力。

Ⅰ、Ⅱ两段柱横截面上的正应力,分别由已求得的轴力和已知的横截面尺寸算得,即

由上述结果可见,砖柱的最大工作应力在柱的下段,其值为0.88MPa,是压应力。

例6-3　一钻杆简图如图6-9(a)所示,上端固定,下端自由,长为l,截面面积为A,材料重度为γ。试分析该杆由自重引起的横截面上的应力沿杆长的分布规律。

解:应用截面法,在距下端距离为x处将杆截开,取下段为分离体,如图6-8(b)所示。设下段杆所受重力为G(x),则有

设横截面上的轴力为FN(x),则有平衡条件

将式(a)代入式(b),得

即FN(x)为x的线性函数。(www.daowen.com)

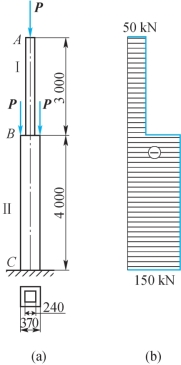
图6-8

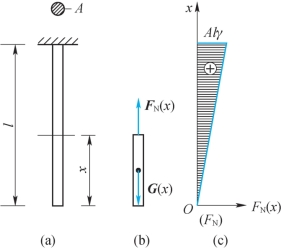
图6-9

x=0时FN(0)=0

x=l时FN(l)=FN,max=Aγl

式中,FN,max为轴力的最大值,即在上端截面轴力最大,轴力图如图6-9(c)所示。那么横截面上的应力为

即应力沿杆长是x的线性函数。

x=0时σ(0)=0

x=l时σ(l)=σmax=γl

式中,σmax为应力的最大值,它发生在上端截面,其分布类似于轴力图。

例6-4　气动吊钩的气缸如图6-10(a)所示,内径D=180mm,壁厚δ=8mm,气压p=2MPa,活塞杆直径d=10mm,试求气缸横截面B—B及纵向截面C—C上的应力。

解:气缸内的压缩气体将使气缸体沿纵横方向胀开,在气缸的纵、横截面上产生拉应力。

(1)求横截面B—B上的应力。取B—B截面右侧部分为研究对象,如图6-10(c)所示,有平衡条件

且D＞＞d时,B—B截面上的轴力为

得B—B截面的面积为

那么横截面B—B上的应力为

σx称为薄壁圆筒的轴向应力。

(2)求纵截面C—C上的应力。取长为l的半圆筒为研究对象,如图6-10(d)所示,由平衡条件

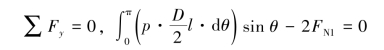
得C—C截面上的内力为

2FN1=plD

C—C截面的面积为

A1=2lδ

当D≥20δ时,可认为应力沿壁厚近似均匀分布,那么纵向截面C—C上的应力为

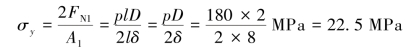
σy称为薄壁圆筒的周向应力。计算结果表明:周向应力是轴向应力的两倍。

图6-10