在研究杆件的强度、刚度等问题时,都需要先求出杆件的内力。关于内力的概念及其计算方法,已在上一章中阐述。如图6-4(a)所示,等直杆在拉力的作用下处于平衡,欲求某横截面m—m上的内力,按截面法,先假想将杆件沿m—m截面截开,留下任一部分作为分离体进行分析,并将去掉部分对留下部分的作用以分布在截面m—m上各点的内力来代替,如图6-4(b)所示。对于留下部分而言,截面m—m上的内力就成为外力。由于整个杆件处于平衡状态,因此杆件的任一部分均应保持平衡。于是,杆件横截面m—m上的内力系的合力(轴力)FN与其左端外力F形成平衡力系,由平衡条件

得

FN为杆件任一横截面上的内力,其作用线与杆件的轴线重合,即垂直于横截面并通过其形心。这种内力称为轴力,用FN表示。

若在分析时取右段为分离体,如图6-4(c)所示,则由作用与反作用公理可知,右段在截面上的轴力与前述左段上的轴力数值相等而方向相反。当然,也可以从右段的平衡条件来确定轴力。

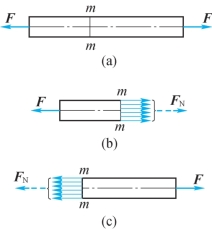
图6-4

对于压杆,同样可以通过上述过程求得其任一横截面上的轴力FN。为了研究方便,给轴力规定一个正负号:当轴力的方向与截面的外法线方向一致时,杆件受拉,规定轴力为正,称为拉力;反之,杆件受压,轴力为负,称为压力。

当杆件受到多个轴向外力作用时,在杆件不同位置的横截面上,轴力往往不同。为了形象而清晰地表示横截面上的轴力沿轴线变化的情况,可用平行于轴线的坐标表示横截面的位置,称为基线;用垂直于轴线的坐标表示横截面上轴力的数值,正的轴力(拉力)画在基线的上侧,负的轴力(压力)画在基线的下侧。这样绘出的轴力沿杆件轴线变化的图线,称为轴力图。

例6-1　一等直杆所受外力如图6-5(a)所示,试求各段截面上的轴力,并作该杆件的轴力图。

解:在AB段范围内任一横截面处将杆件截开,取左段为分离体,如图6-5(b)所示,假定轴力FN1为拉力(以后轴力都按拉力假设),由平衡方程

∑Fx=0,FN1-30=0

得

FN1=30kN

结果为正值,故FN1为拉力。(www.daowen.com)

同理,如图6-5(c)所示,可求得BC段内任一横截面上的轴力为

FN2=(30+40)kN=70kN

在求CD段内的轴力时,将杆件截开后取右段为分离体,如图6-5(d)所示,因为右段杆件上包含的外力较少。由平衡方程

∑Fx=0,　-FN3-30+20=0

得

FN3=(-30+20)kN=-10kN

结果为负值,说明FN3为压力。

同理,可得DE段内任一横截面上的轴力FN4为

FN4=20kN

按上述作轴力图的规则,作出杆件的轴力图,如图6-5(f)所示。FN,max发生在BC段内的任一横截面上,其值为70kN。

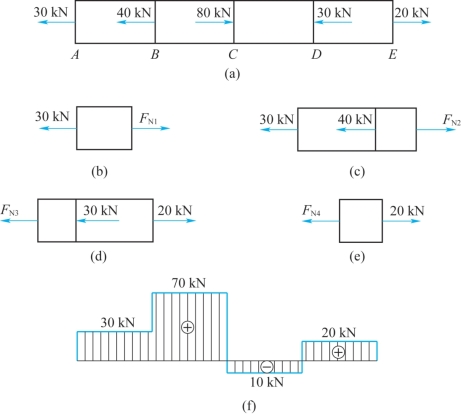
图6-5

由上述计算可见,在求轴力时,先假设未知轴力为拉力,则得数前的正负号,既表明所设轴力的方向是否正确,也符合轴力的正负号规定,因而不必在得数后再注“压”或“拉”字。

思政提示

轴力是对杆件某个截面处内力的衡量,并不能表征整个杆件的受力情况,轴力图则是从整体角度观察杆件,提出危险截面的所在。因此,要站在整体角度看问题,从宏观角度审视情况的发展和变化,并以此来指导局部的工作,不能鼠目寸光,只关注眼前的情况而忽略观察变化的趋势。