经过对前面小节的学习,我们知道在外力作用下,各点的应力一般是不一样的。与之类似,各点变形的程度也不一样。为了研究构件的变形情况,我们把构件假想成众多微小的正六面体(若六面体的边长趋于无限小则称为单元体),构件的变形可以看作所有单元体变形积累后的结果。而单元体的变形则只表现为边长的改变与直角的改变两种。为了度量各点的变形程度,需要定义线应变和切应变两个基本物理量。

图5-3(a)所示为点K处的单元体。单元体沿x轴的棱边原长为Δx,变形后长度为Δx+Δu,如图5-3(b)所示,比值

表示线段KB每单位长度的平均变化,称为平均线应变。让Δx趋近于0,极限

称为点K沿x方向的线应变或正应变,简称为应变。类似地,可以定义沿y和z方向的应变。线应变是无量纲量。(www.daowen.com)

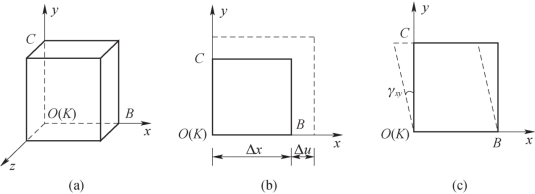
图5-3

单元体互相垂直的两条棱边所夹直角的改变量称为切应变,也称角应变或者剪应变,用γ表示。图5-3(c)中γxy即为点K在xy平面内的切应变。类似地,也可以定义在xz平面和yz平面内的切应变。切应变也是无量纲量,常用弧度度量。

还应该指出,构件的变形通常是非常微小的。材料力学研究的变形也局限于小变形,即变形尺寸远小于物体原始尺寸,这就是小变形条件。在小变形条件下,当研究构件平衡和构件内部受力时,都可以不考虑变形的影响而仍按照原始尺寸分析计算,这使问题得以大大简化。

思政提示

不同尺寸杆件之间的变形量不能直接反应其变形程度。同样,人与人之间的情况各不相同,不能硬性地拿某一指标强行对比,更不能进行盲目攀比,而应当立足现实情况,关注自身的发展,脚踏实地地提高自身素质、修养和文化,一步一个脚印地迈向成功。