1)简单几何形状物体的重心

对于均质物体,其有对称面、对称轴或对称中心,则重心在这个对称面、对称轴或对称中心上。类似的简单几何形状物体的重心可查工程手册得到。型钢(如工字钢、槽钢、角钢等)的截面形心,可查型钢表得到。

2)试验法测定重心的位置

工程中一些外形复杂或质量分布不均的物体很难用计算方法求其重心,此时可用试验方法测定重心位置。下面介绍两种方法。

(1)悬挂法:如图4-10所示,如果需求一薄板的重心,可先将板挂于任一点A,根据二力平衡条件,重心必在过悬挂点的铅垂上,可在板上画出此线。然后,将板悬挂于另一点,同样画出另一直线,两线交点就是重心。

(2)称重法:如图4-11所示,以汽车为例简述测定重心的方法称出汽车重P,测出前后轮距离l,车轮半径r,为测定xc,将一轮放在地面上,一轮放在磅秤上,如磅秤读数为F。由汽车平衡,列其平衡方程

∑MA(F)=0,Pxc-Fl=0

解得xc=Fl/P。

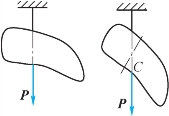
图4-10

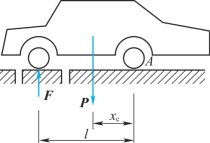
图4-11

3)用分割法求重心

例4-6　平面图形形状及尺寸如图4-12所示,试确定其形心坐标。

(1)用分割法求解,图形分割及坐标如图4-12(a)所示,则

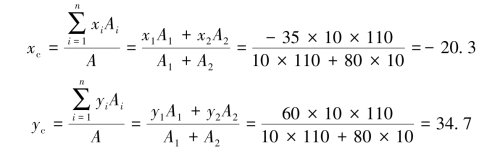
(2)用负面积法求解,图形分割及坐标如图4-12(b)所示。则

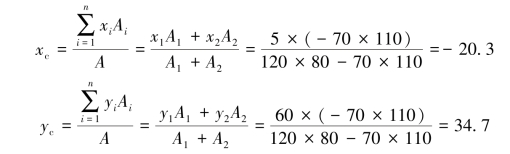
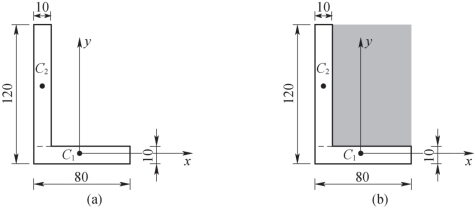
图4-12

思政提示

当物体密度均匀时,重心和形心是重合的;而密度不均匀时,重心和形心不重合。说明任何真理都是在一定范围、一定条件下才能成立的,如果超出这个范围,失去了特定条件,它就有可能变成谬误。

习　题

4-1　桁架尺寸及受力如题4-1图所示,求出各杆内力,图中长度单位为m。

4-2　桁架尺寸及受力如题4-2图所示,求出各杆内力。

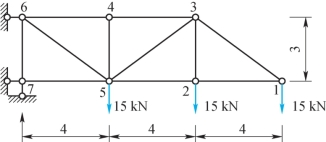
题4-1图

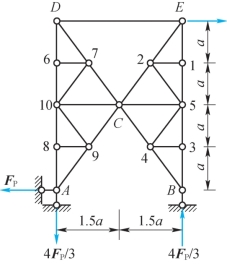
题4-2图

4-3　桁架尺寸及受力如题4-3图所示,求出杆a、b的内力。

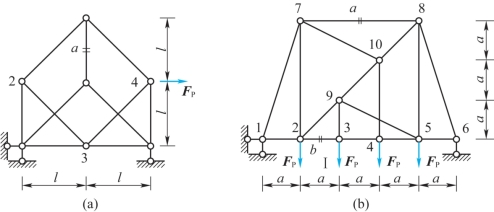
题4-3图

4-4　桁架尺寸及受力如题4-4图所示,求出杆1、2的内力,图中长度单位为m。

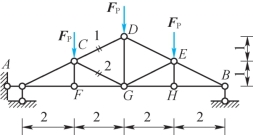
题4-4图

4-5　如题4-5图所示,重500N的物体A置于重400N的物体B上,B又置于水平面C上。已知fAB=0.3,fBC=0.2,今在A上作用一与水平面成30°的力F。问:当力F逐渐加大时,是A先滑动呢,还是A、B一起滑动?如果物体B重为200N,情况又如何?(www.daowen.com)

4-6　如题4-6图所示,欲转动一置于V形槽中的棒料,需作用一力偶,力偶矩M=1500N·cm,已知棒料重G=400N,直径D=25cm。试求棒料与V形槽之间的静摩擦因数fs。

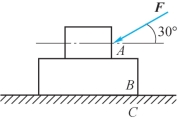
题4-5图

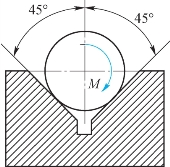
题4-6图

4-7　砖夹宽280mm,爪AHB和BCED在点B处铰接,如题4-7图所示。被提起的砖重力为G,提举力F作用在砖夹中心线上。若砖夹与砖之间的静摩擦因数fs=0.5,则尺寸b应为多大,才能保证砖被夹起时不滑掉?

4-8　在用铰链O固定的木板AO和BO间放一重W的匀质圆柱,并用大小等于P的两个水平力P1与P2维持平衡,如题4-8图所示。设圆柱与木板间的摩擦因数为f,不计铰链中的摩擦力以及木板的质量,求平衡时P的范围。

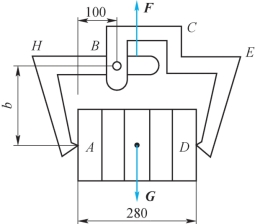
题4-7图

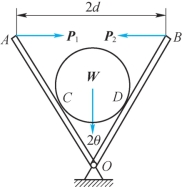
题4-8图

4-9　有两种制动装置如题4-9图所示。已知圆轮上转矩为M,几何尺寸a、b、c,圆轮和制动块K间的静摩擦因数为fs。试求制动所需的最小力F的大小。

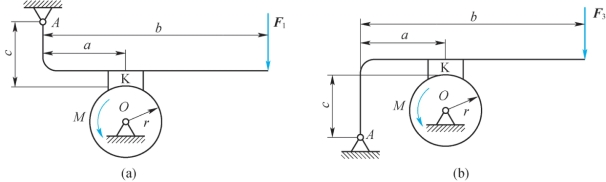
题4-9图

4-10　试求题4-10图中阴影线平面图形的形心坐标。

4-11　试求题4-11图中阴影线平面图形的形心坐标。

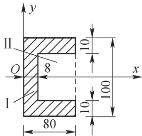
题4-10图

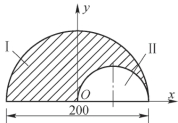
题4-11图

4-12　试求题4-12图中阴影线平面图形的形心坐标。

4-13　试求题4-13图中阴影线平面图形的形心坐标。

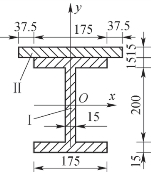
题4-12图

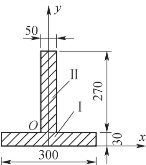
题4-13图

4-14　试求题4-14图中阴影线平面图形的形心坐标。

4-15　如题4-15图所示为混凝土水坝截面简图,求其形心位置。

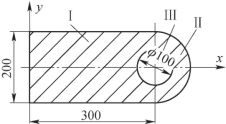
题4-14图

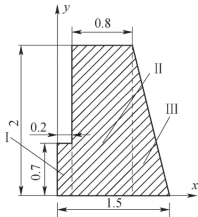
题4-15图

4-16　试求题4-16图所示平面图形的形心位置,图中尺寸单位为mm。

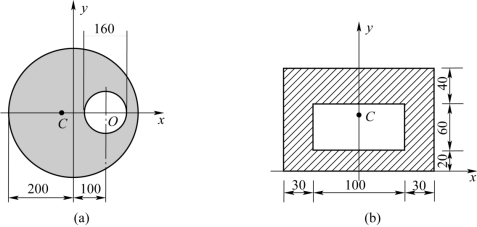
题4-16图