两个表面粗糙的物体,当接触面间有相对滑动趋势或相对滑动时,彼此作用有阻碍相对滑动趋势或相对滑动的阻力,作用位置为相互接触处,方向与相对滑动趋势或相对滑动方向相反,大小随主动力的不同而不同,分以下3种情况:

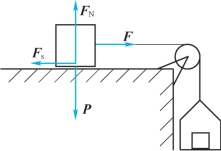
图4-6

(1)静滑动摩擦力,简称静摩擦力。如图4-6所示,当绳中拉力F较小时,物体保持静止。支撑面对物体除了法向约束反力以外,还有切向约束反力,即静滑动摩擦力Fs,其方向与物体相对滑动趋势相反,大小由平衡条件确定。

(2)最大静滑动摩擦力,简称最大静摩擦力。图4-6中,当绳中拉力F大到一定数值时,物体处于将要滑动、但尚未开始滑动的临界平衡状态,静摩擦力达到最大。静摩擦力与一般约束反力不同,它并不随拉力F的增大而无限度地增大。试验证明:Fmax=fsFN,也就是静摩擦定律(又称库仑摩擦定律),是工程中常用的近似理论。fs称为静摩擦因数,无量纲,可查工程手册得到。它与接触物体的材料和表面情况有关,与接触面的大小无关。例如,汽车一般用后轮驱动,因为后轮压力大于前轮,这样可以允许产生较大的向前推动的摩擦力;火车在下雪后行驶时,要在铁轨上洒细沙,以增大摩擦因数,避免打滑。

(3)动滑动摩擦力,简称动摩擦力。当静滑动摩擦力已达到最大时,若主动力F再继续加大,接触面之间将出现相对滑动,此时,接触面间仍作用有相对滑动的阻力,这种阻力称动滑动摩擦力。试验表明:Ff=fFN,其中,f为动摩擦因数,一般f＜fs。动摩擦因数与接触物体的材料和表面情况有关,多数情况下,动摩擦因数随相对滑动的速度的增大而稍减小,但当相对速度变化不大时,动摩擦因数可近似认为是常数。

考虑摩擦时,支撑面对物体的作用力不仅有法向反力FN,还有摩擦力Fs,二者的合力称为支撑面对物体的全约束反力。它与接触面的法线成某一角度φ。当拉力逐渐增大时,静摩擦力也随着增大,φ角也相应增大,当拉力增大到临界值时,摩擦力达到最大静摩擦力Fmax,此时全约束反力与法线间的夹角也达到最大值ρ,ρ称为摩擦角。试验证明,静摩擦因数等于摩擦角的正切,即fs=tanρ。可见ρ与f一样,也是表示物体材料摩擦性质的物理量。

由摩擦角的这一性质可知,如果作用于物体的主动力的合力的作用线在摩擦角之内,则不论这个力有多大,总有一个全反力与之平衡,物体保持静止;反之,如果主动力的合力的作用线在摩擦角之外,则无论这个力如何小,物体也不可能保持平衡。这种与力的大小无关而与摩擦角(摩擦因数)有关的平衡条件称为自锁条件,物体在这种条件下的平衡现象称为自锁现象。

考虑摩擦时,求解物体平衡问题的步骤与前几章所述大致相同,但有如下的几个特点:(1)分析物体受力时,必须考虑接触面间切向的摩擦力,通常增加了未知量的数目;(2)为确定这些新增加的未知量,还需列出补充方程,即Ff=fFN,补充方程的数目与摩擦力的数目相同;(3)由于物体平衡时摩擦力有一定的范围(即0≤Fs≤fsFN),所以有摩擦时平衡问题的解亦有一定的范围,而不是一个确定的值。

工程中有不少问题只需要分析平衡的临界状态,这时静摩擦力等于其最大值,补充方程只取等号。有时为了计算方便,也先在临界状态下计算,求得结果后再分析、讨论其解的平衡范围。

例4-4　如图4-7所示,将重为P的物块放在斜面上,斜面倾角α大于接触面的摩擦角,已知静摩擦系数为fs,若加一水平力F使物块平衡,求力F的范围。

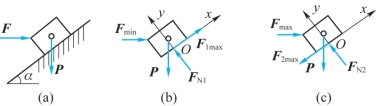
图4-7

解:以物块为研究对象,当物块处于向下滑动的临界平衡状态时,受力如图4-7(b)所示,建立Oxy坐标系。列平衡方程

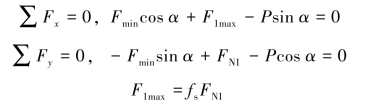
解得Fmin=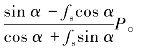(www.daowen.com)

当物块处于向上滑动的临界平衡状态时,受力如图4-7(c)所示。列平衡方程

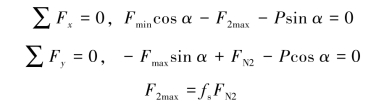
解得Fmax=

故力F应满足的条件为

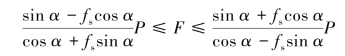
例4-5　如图4-8所示,梯子AB长为2a,重为P,其一端置于水平面上,另一端靠在铅垂墙上。设梯子与地和墙的静摩擦因数均为fs,问梯子与水平线的夹角α为多大时,梯子能处于平衡?

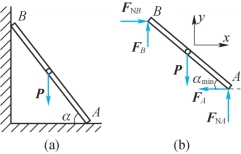
图4-8

解:以梯子为研究对象,当梯子处于向下滑动的临界平衡状态时,受力图如图4-8(b)所示,此时α角取最小值。建立如图所示坐标系,列平衡方程

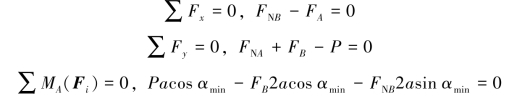
由摩擦定律得

且

解得2φm。

此条件即为梯子的自锁条件。