平面任意力系平衡的充分必要条件:力系的主矢和对任意点的主矩同时等于0,即

由主矢和主矩的定义,进一步可得

于是得平面任意力系平衡的解析条件:平面任意力系中各力在力系所在平面垂直的两个坐标轴投影的代数和为0,各力对任意点的矩的代数和为0。式(3-3)为平面任意力系的平衡方程,包括3个独立方程,最多只能解3个未知力。为书写方便,通常将其简写为

从另一个角度也可以得到和解释其平衡方程:平面中的物体会有3个自由度,必须限制其沿两个坐标轴方向的位移和绕垂直于平面法线方向的转动,才能够达到平衡,也就是必须满足式(3-3)。

式(3-3)为平面任意力系平衡方程的基本形式,还有其他两种形式的方程

式(3-4)为二力矩式平衡方程,适用条件为A、B连线不能与x轴垂直。式(3-4)后两式为合力矩等于0,说明合力的作用线通过A、B两点连线,但x轴不与A、B连线垂直,以保证力系中的合力为0。

还可以有以下形式的平衡方程

式(3-5)为三力矩式平衡方程,适用条件为A、B、C三点不共线。

值得注意的是,虽然有3种形式的平衡方程,但求解时应根据具体问题而定,只能选择其中的一种形式,且对于特定的研究对象只能列3个平衡方程,求解3个未知力。若列第四个方程,则它是不独立的,是前3个方程的线性组合;若需要求解更多的未知力,只能再选其他物体为研究对象,进而列其平衡方程进行求解。同时,为方便求解,应尽可能地使一个方程含有一个未知力,避免联立求解。

例3-5　图3-4(a)所示水平梁AB,A端为固定铰链支座,B端为一滚动支座。梁长为4a,梁重为P,作用在梁的中点C。在梁的AC段上受均布载荷q作用,在梁的BC段上受力偶作用,力偶矩M=Pa。求A和B处的支座约束力。

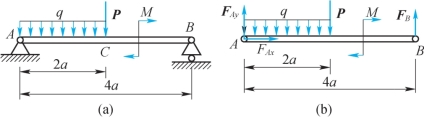
图3-4

解:(1)选梁AB为研究对象,作用在其上的主动力有均布载荷q,力偶矩为M;约束反力为固定铰支座A端的FAx、FAy两个分力,滚动支座B端的铅垂向上的法向力FB,如图3-4(b)所示。

(2)建立坐标系,列平衡方程:

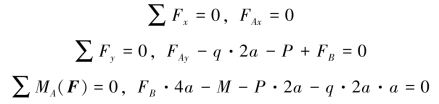(www.daowen.com)

解得FAx=0,FAy=

如果结果中的力含有负号,说明原假设方向与实际方向相反。

例3-6　如图3-5(a)所示,梁受集中力F和分布载荷q作用,求A、B支座约束反力,长度单位为m。

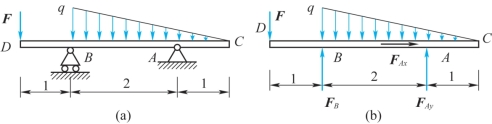
图3-5

解:(1)选梁CD为研究对象,作用在它上的主动力有:分布载荷q,集中力F;约束反力为固定铰支座A端的FAx、FAy两个分力,滚动支座B端的铅垂向上的法向力FB,如图3-5(b)所示。

(2)建立坐标系,列平衡方程

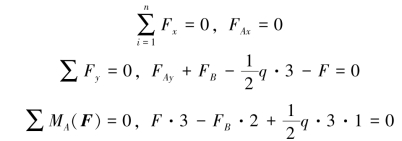
解得FB=

例3-7　刚性支架的A端嵌固在基础上,C端装有滑轮,如图3-6(a)所示。绳子一端固定在点D,与水平面夹角为α=60°,另一端吊着重Q=1000N的重物。已知AD=0.5m,DE=1.5m。求支架插入端的约束反力(包括反力偶在内)。

解:取整个支架为研究对象。受力图如图3-6(b)所示。已知滑轮两边绳子的拉力相等,即T=Q=1000N。选坐标轴如图3-6(b)所示,则平衡方程为

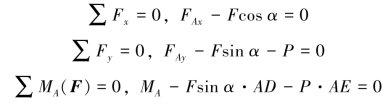
解得FAx=500N,FAy=1866N,MA=2433N·m。

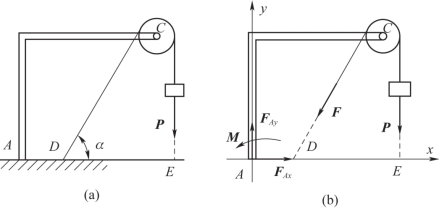
图3-6

讨论:(1)遇到带有滑轮的结构,一般不把滑轮拆开,以免增加不需求的未知数。本例采用基本形式的平衡方程组,每个平衡方程都只有一个未知数,不用解联立方程,求解最简便。若采用二矩或三矩形式各平衡方程不都是只有一个未知数,需要解联立方程。

(2)本例先用字符列平衡方程并求解,最后代入数值,这样能减少计算错误,便于复查。一般不要先用数字列方程。

思政提示

平面任意力系的平衡是平面力系平衡的普遍形式,平面汇交力系和平面力偶系的平衡是平面任意力系平衡的特例。同样地,任何事物都具有普遍性和特殊性,在这种状态下,双方的制约保持在一定的范围之内,此时事物彼此处于量变的积累状态,即相对静止;如果事物双方的制约超过了这个度的范围,它们所处的这个系统将会发生质变,形成一个新的系统,在这个新的系统下保持相对的平衡,处于另一个相对静止状态(量变的状态)。