本章开头由自由度的角度得到平面汇交力系有2个平衡方程。这里从另一个角度来得到平面汇交力系平衡方程,其平衡的充分必要条件是平面汇交力系的合力为0,亦即其主矢等于0。由第2章主矢的定义可得

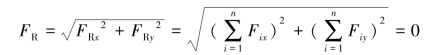
从而得平面汇交力系平衡方程

式(3.1)即为平面汇交力系平衡的解析条件,可表述为力系中各力在直角坐标轴上的投影的代数和均为0。由于式(3-1)包含两个独立方程,因此可求解两个未知力。

例3-3　杆AC、BC在C处铰接,另一端均与墙面铰接,如图3-3(a)所示,F1和F2作用在销钉C上,F1=445N,F2=535N,不计杆重,试求两杆所受的力。

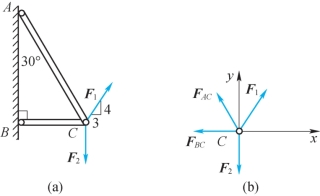
图3-3

解:(1)由于杆AC、BC不计自重,因此二者皆为二力构件,如果取二力构件为研究对象,则所列平衡方程中没有已知量,解不出有用结果。所以,在平衡问题中一般不取二力构件为研究对象,这里取节点C为研究对象,画受力图如图3-3(b)所示。

(2)列平衡方程如下(www.daowen.com)

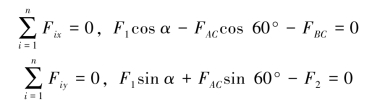
解得FAC=206.7N,FBC=341.7N。

若所得的结果为正值,说明原假设与实际方向相同,即杆AC与BC均受拉;若所得的结果为负值,说明原假设与实际方向相反,杆AC与BC均受压。

例3-4　用解析法求解例3-1。

(1)取杆AB为研究对象,受力图同图3-1。

(2)以点C为坐标原点建立坐标系,列平衡方程如下

解得FD=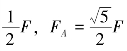=1.12F,结果与例3-1相同。

思政提示

求解平面汇交力系的平衡有几何法和解析法两种方法,每种方法各有其适用范围和优缺点,如:几何法直观、容易理解;解析法运算方便等。因此,我们在生活、学习中遇到困难时,要学会分析问题,找到最佳并适合自己的方法,克服困难、解决问题,达到事半功倍的效果。