(1)当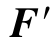 R=0,MO≠0时,简化为一个力偶。此时,力偶矩与简化的位置无关,主矩MO为原来力系的合力偶矩。
R=0,MO≠0时,简化为一个力偶。此时,力偶矩与简化的位置无关,主矩MO为原来力系的合力偶矩。
(2)当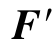 R≠0,MO=0时,简化为一个力。此时,主矢为原来力系的合力,合力的作用线通过简化中心。
R≠0,MO=0时,简化为一个力。此时,主矢为原来力系的合力,合力的作用线通过简化中心。
(3)当 ≠0,MO≠0时,可进一步简化为一个力。如果将力的平移定理的证明过程倒过来看,也就是通过平移主矢产生的力偶与主矩抵消掉而只剩下一个力,此力即为原来力系的合力,如图2-14所示。合力的作用线到点O的距离为
≠0,MO≠0时,可进一步简化为一个力。如果将力的平移定理的证明过程倒过来看,也就是通过平移主矢产生的力偶与主矩抵消掉而只剩下一个力,此力即为原来力系的合力,如图2-14所示。合力的作用线到点O的距离为


图2-14
(4)当 =0,MO=0时,平面任意力系为平衡力系。
=0,MO=0时,平面任意力系为平衡力系。
由上面(2)、(3)可以看出,不论主矩是否等于0,只要主矢不等于0,力系最终都可以简化为一个合力。
例2-6 简支梁受三角形载荷作用,最大载荷集度为qo(单位:N/m),如图2-15所示,求其合力的大小和作用线的位置。

图2-15
解:设梁距A端x处的载荷集度为q,其值为![]() 则微段dx上所受的载荷为
则微段dx上所受的载荷为
![]()
简支梁所受三角形载荷的合力为

设合力作用线距A端为d,由合力矩定理得

联立以上两式,得合力作用线距A端的距离为

例2-7 已知F1=150N,F2=200N,F3=300N,F= =200N,如图2-16(a)所示。求力系向点O的简化结果,并求力系合力的大小及其与原点O的距离。
=200N,如图2-16(a)所示。求力系向点O的简化结果,并求力系合力的大小及其与原点O的距离。

图2-16
解:(1)将力系向O简化,求得主矢 和主矩MO。即
和主矩MO。即
主矢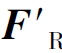 在x、y轴上的投影为
在x、y轴上的投影为

主矢 的大小为
的大小为
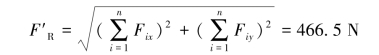
主矢 的方向余弦为
的方向余弦为

则方向角为
![]()
故主矢量 在第Ⅲ象限内,与x轴的夹角为-20.28°。
在第Ⅲ象限内,与x轴的夹角为-20.28°。
力系对简化中心O的主矩MO为

主矢 和主矩MO方向如图2-16(b)所示。
和主矩MO方向如图2-16(b)所示。
(2)求合力FR作用线的位置。由于合力FR与主矢 大小相等方向相同,因此其作用线与x轴交点的坐标可根据合力矩定理求得,如图2-16(c)所示,即
大小相等方向相同,因此其作用线与x轴交点的坐标可根据合力矩定理求得,如图2-16(c)所示,即
![]()
解得

合力FR作用线的位置如图2-16(c)所示。
例2-8 已知:P1=450kN,P2=200kN,F1=300kN,F2=70kN,长度单位为m,如图2-17(a)所示。求力系向点O简化的结果,合力与OA的交点到点O的距离为x。

图2-17
解:(1)将力系向O简化,求得主矢 和主矩MO。
和主矩MO。
![]()
主矢 在x、y轴上的投影为
在x、y轴上的投影为

主矢 的大小为
的大小为
![]()
主矢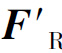 的方向余弦为
的方向余弦为
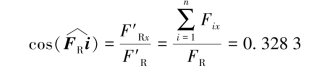

则方向角为
![]()
故主矢 在第Ⅳ象限内,与x轴的夹角为-70.84°。
在第Ⅳ象限内,与x轴的夹角为-70.84°。
力系对简化中心O的主矩MO为(https://www.daowen.com)

主矢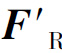 和主矩MO的方向如图2-17(b)所示。
和主矩MO的方向如图2-17(b)所示。
(2)求合力FR作用线的位置。由于合力FR与主矢 大小相等方向相同,因此其作用线与x轴交点的坐标可根据合力矩定理求得,如图2-17(c)所示,即
大小相等方向相同,因此其作用线与x轴交点的坐标可根据合力矩定理求得,如图2-17(c)所示,即
![]()
解得

合力FR作用线的位置如图2-17(c)所示。
思政提示
平面力系不管多么复杂,利用力的平移定理最终都可简化为一个主矢和一个主矩。生活和工作中遇到的难题不管多么复杂,只要认真分析和观察,找到事物的内在规律,抓住根本去伪存真,将复杂的问题简单化,最终一定可以找到解决办法。
习 题
2-1 如题2-1图所示,力F作用于圆盘且与圆盘共面,圆的半径为r,角α、β、γ均为已知,试求力F对点A的矩。
2-2 如题2-2图所示为一起重吊钩,若吊钩点O处所承受的力偶矩最大值为5kN·m,为保证吊钩不发生倾斜,起吊重量不能超过多少?

题2-1图

题2-2图
2-3 求题2-3图中平行分布力的合力和对于点A之矩。

题2-3图
2-4 齿轮分度圆半径为r,工作时受到的啮合力F=1000N,方向如题2-4图所示。试求:力F对y轴的矩。
2-5 在正方体的顶角A和B处,分别作用力F1和F2,如题2-5图所示。求此两力在x、y、z轴上的投影和对x、y、z轴的矩。并将图中的力系向点O简化,用解析式表示主矢、主矩的大小和方向。
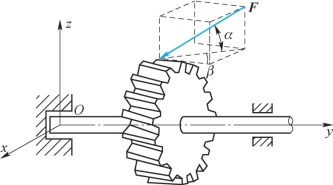
题2-4图

题2-5图
2-6 已知连杆结构AB上作用一力偶,力偶矩为M,杆重不计。求在题2-6图(a)(b)两种情况下,支座A和B的约束反力。

题2-6图
2-7 如题2-7图所示,两曲杆自重不计,曲杆AB上作用有主动力偶,其力偶矩为M,试求A和C点处的约束反力。
2-8 如题2-8图所示,各构件的自重略去不计,在构件BC上作用一力偶矩为M的力偶,各尺寸如图。求支座A的约束反力。
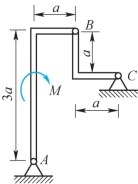
题2-7图

题2-8图
2-9 构件的支承及载荷如题2-9图所示,求支座A、B处的约束反力。
2-10 铰链四连杆机构在题2-10图所示位置平衡,已知OA=0.4m,O1B=0.6m,作用在曲柄OA上的力偶矩M1=1N·m,不计杆重,求力偶矩M2的大小及连杆AB所受的力。

题2-9图
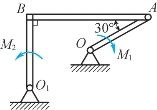
题2-10图
2-11 如题2-11图所示,两个尺寸相同的直角曲杆受相同的力偶M作用,则A1和A2处约束反力分别为多少?

题2-11图
2-12 分析题2-12图所示平面任意力系向点O简化的结果,图中长度单位为cm。已知:F1=100N,F2=150N,F3=200N,F4=250N,F=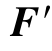 =50N。
=50N。
2-13 如题2-13图所示,已知F1=150N,F2=200N,F3=300N,F= =200N。求力系向点O简化的结果,并求力系合力的大小及其与原点O的距离d,图中长度单位为cm。
=200N。求力系向点O简化的结果,并求力系合力的大小及其与原点O的距离d,图中长度单位为cm。

题2-12图

题2-13图
2-14 铆接薄钢板在孔心A、B和C处受三力作用,如题2-14图所示,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果,长度单位为cm。
2-15 求题2-15图所示平面力系的合成结果,长度单位为m。
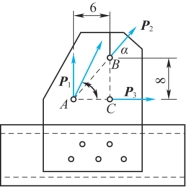
题2-14图
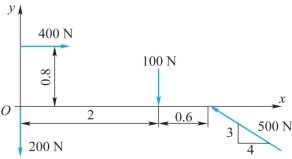
题2-15图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






