力对轴之矩是度量力使物体绕某特定轴的转动效应的力学量。实践表明,力使物体绕轴转动的效果,不仅与力的大小有关,而且和力与转轴之间的相对位置有关。在几何上,一条射线(力)和一条直线(轴)不一定在同一个平面,因此,力对轴之矩为空间问题。

图2-4

如图2-4所示,设作用在刚体上的力F的作用点为A,将力F分解为两个分力,其中一个分力Fz∥Oz,另一个分力Fxy在过a且垂直于Oz轴的平面xy内。由经验知:分力Fz不会使刚体绕Oz轴转动,正如作用在门上的重力不会使它绕铅垂的门轴转动一样,力F对刚体绕Oz轴的转动完全取决于分力Fxy对点O之矩,于是力对轴之矩就是力在垂直于该轴的平面上的分力对该轴与平面交点之矩,即

由此可见,力对轴之矩是力使刚体绕该轴转动效应的量度,其大小等于力在垂直于该轴的平面上的投影对该平面与该轴的交点之矩。其正负号规定为:从轴的正向看,力使物体绕该轴逆时针转动时,取正号;反之,取负号。也可按右手螺旋法则来确定其正负号,拇指指向与轴的正向一致时取正号,反之取负号。注意,当力与轴共面时力对该轴之矩为0。

力对轴之矩的单位与力对点之矩是一样的,即N·m或kN·m。另外,合力矩定理在空间力系中也同样适用。式(2-5)可以表示为

同理可得,力F对另外两轴的力矩分别为

(www.daowen.com)

例2-3　构件OA在点A受到作用力F=1000N,方向如图2-5所示。图中点A在Oxy平面内,尺寸如图所示,长度单位为m。试求:力F对x、y、z坐标轴的矩。

图2-5

解:力F在x、y、z轴上的投影分别为

力F对x、y、z轴之矩分别为

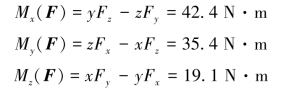
力F对x、y、z轴之矩也可以用力对轴之矩的定义计算,请读者自行练习。

思政提示

当力的大小和方向一定时,力臂越大力矩就越大,对物体的转动效应也就越大。同样,当我们做一件事情时,要学会利用身边的有利条件和资源,让同样的付出收到最大的成效。