在利用力矩的定义计算力对点之矩时,有的时候力臂的大小在几何上不是很好计算,此时可用合力矩定理进行求解。
合力矩定理:平面汇交力系的合力对其平面内任一点之矩等于所有分力对同一点之矩的代数和,即
![]()
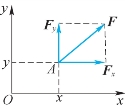
图2-2
根据此定理,将力F沿坐标分解得分力Fx、Fy,如图2-2所示,则力对点之矩解析表达式为
![]()
合力对点之矩解析表达式为
![]()
合力矩定理建立了合力对点之矩与分力对同一点之矩的关系,这个定理也适用于有合力的其他力系。
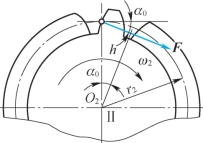
图2-3
例2-1 齿轮分度圆半径为![]() ,压力角为α0,受力图如图2-3所示,试求力F对点O2之矩。
,压力角为α0,受力图如图2-3所示,试求力F对点O2之矩。
解:本题有两种解法。
(1)根据力矩的定义计算力F对点O2之矩。
先求力臂h,从图中的几何关系得
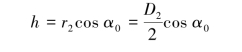
所以,力F对点O2之矩为(www.daowen.com)
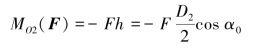
(2)根据合力矩定理计算力F对点O2之矩。
将力F在点C分解为两个正交的分力,由合力矩定理可得
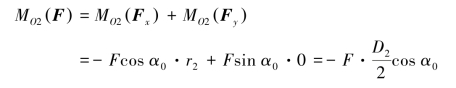
本例两种解法的计算结果是相同的,当力臂不易确定时,用合力矩定理较为简单。
例2-2 如图1-3所示,简支梁分别受均布载荷和三角载荷作用时,假设梁的跨度为l,分别求出两种载荷对点A和点B的力矩。
解:本题有两种解法。
(1)根据分布载荷的定义,利用微积分的原理,在距离点A为x处取一微段,则该段上均布载荷的微力为qdx,该段上三角载荷的微力为![]() 则
则
均布载荷对点A和点B的力矩分别为
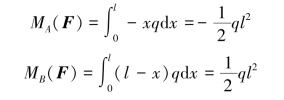
三角载荷对点A和点B的力矩分别为
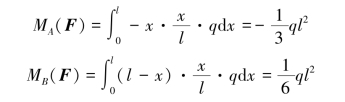
利用上述方法求解分布载荷的力矩虽然思路明确,但是计算过程比较复杂,对学生的数学计算能力要求较高。在实际计算中可利用下述简便方法计算。
(2)等效载荷法。分布载荷的合力大小在2.1节已经求出,因此可将分布载荷视为作用在一个等效作用点上的集中载荷,只要能找到分布载荷的等效作用点,即可根据力对点之矩的定义求出分布载荷对某点的力矩。对于均布载荷,其等效作用点在载荷跨度的中点处;而三角载荷的等效作用点在距离q=0点的2/3跨度处,此结论将在例2-6中予以证明。因此,不难求出均布载荷对点A和点B的力矩分别为
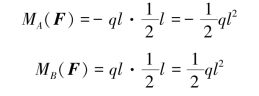
三角载荷对点A和点B的力矩分别为
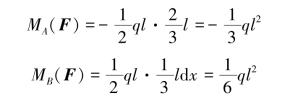
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






