单位矩阵解耦法是对角矩阵解耦法的特殊情况，要求被控对象特性矩阵与解耦器矩阵的乘积等于单位矩阵。即

因此，系统输入输出方程满足如下关系

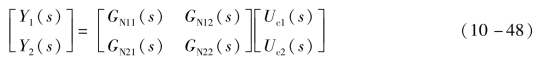
于是得解耦器的数学模型为

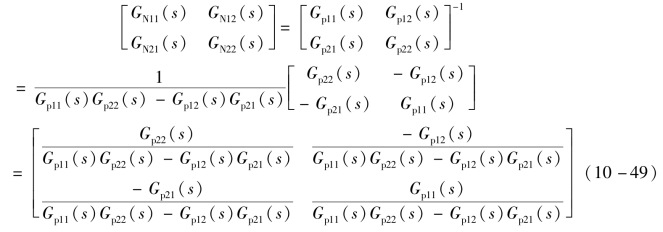
同理可以证明，U c1（s）对Y2（s）影响等于0，U c2（s）对Y1（s）影响等于0，即U c1（s）对Y2（s）之间、U c2（s）对Y1（s）之间的耦合关系已被解除。图10-17是利用单位矩阵解耦得到的2个彼此独立的等效控制系统的方框图。

图10-17　单位矩阵解耦后的等效控制系统的方框图

综上所述，采用不同的解耦方法都能达到解耦的目的，但是采用单位矩阵解耦法的优点更突出。对角矩阵解耦法和前馈补偿解耦法得到的解耦效果和系统的控制品质是相同的，这两种方法都是设法解除交叉通道，并使其等效成两个独立的单回路控制系统。而单位矩阵解耦法，除了能获得优良的解耦效果之外，还能提高控制品质，减少动态偏差，加快响应速度，缩短调节时间。值得注意的是，本节介绍的几种解耦设计方法，一般都要涉及解耦器或控制器与被控对象之间零点/极点抵消问题，这在某些情况下可能会引起系统不稳定，或是解耦器是物理不可实现的。因此，如果遇到这类问题比较严重，建议采用其他解耦方法，如非零点/极点抵消解耦法等。

必须指出的是，多变量解耦有动态解耦和稳态解耦之分。动态解耦的补偿是时间补偿，而稳态解耦的补偿是幅值补偿。由于动态解耦要比稳态解耦复杂得多，因此一般只在要求较高、解耦器又能实现的条件下使用。当被控对象各通道的时间常数非常接近时，采用稳态解耦一般都能满足要求。由于稳态解耦结构简单、易于实现、解耦效果较佳，故稳态解耦在很多场合得到了广泛的应用。

【例10-4】现有某混凝土快干性和强度控制系统，其中混凝土快干性和强度受到纯原料量和含水量的影响，系统的输入量为纯原料量和含水量，系统的输出量为混凝土的快干性和强度，系统输入与输出之间的传递函数矩阵为

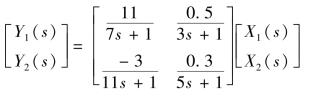
试采用对角矩阵解耦法求出解耦控制器，并对该系统进行控制仿真。

解：（1）求系统相对增益及系统耦合分析。

由已知输入输出之间的传递函数矩阵可得系统稳态放大系数矩阵为

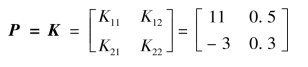
系统相对增益矩阵为(www.daowen.com)

由相对增益矩阵可以看出，控制系统输入输出的配对选择正确，但通道间存在较强的相互耦合，需要对系统进行解耦设计。

（2）确定解耦控制器。

根据式（10-45）求解的对角矩阵含有s的4次方项，实际构造时结构复杂、计算量大，对此进行改进。令

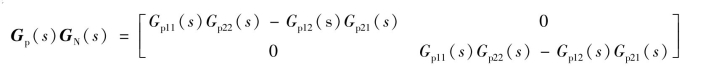
则解耦装置G N（s）为

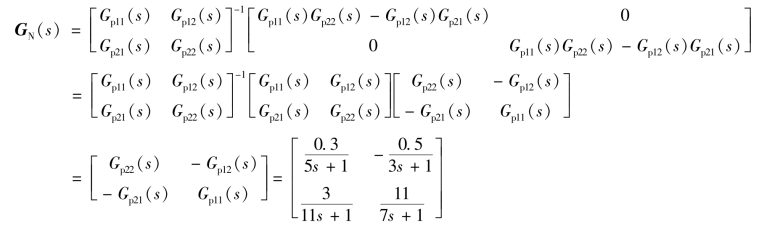
（3）仿真结果比较。

系统存在耦合时，其Simulink仿真图如图10-18所示。采用经验法对PI控制器进行参数整定。当x1 y1通道K c1＝2、T i1＝100，x2 y2通道K c2＝1.6、T i2＝60时，整个系统的阶跃响应曲线如图10-19所示。可能看出，耦合对系统动态特性造成了一定影响，使x2 y2通道的动态品质变差。

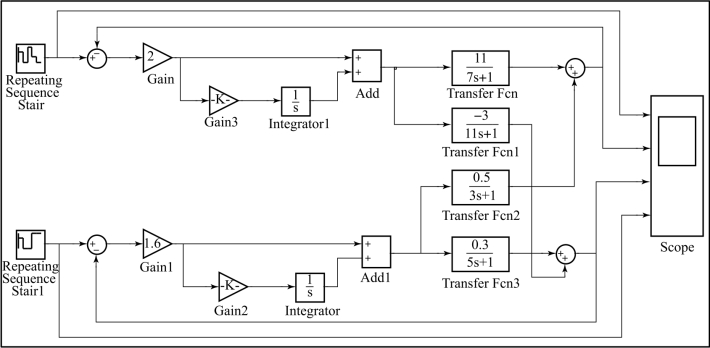
图10-18　系统存在耦合时的Simulink仿真图

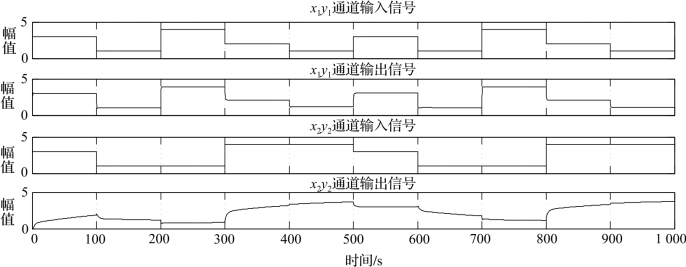
图10-19　系统存在耦合时的阶跃响应曲线

采用对角矩阵解耦后整个系统的Simulink仿真图如图10-20所示，通过经验法整定两个PI控制器的参数，当K c1＝2、T i1＝150、K c2＝1.6、T i2＝60时，其Simulink仿真结果如图10-21所示。由图可见，系统实现了系统的解耦。

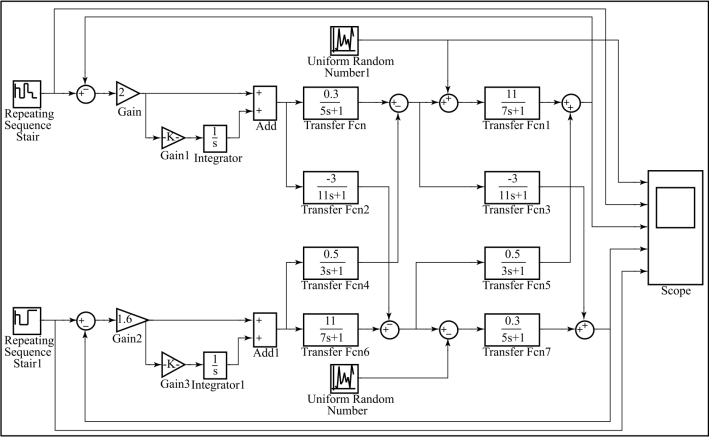
图10-20　解耦系统的Simulink仿真框图

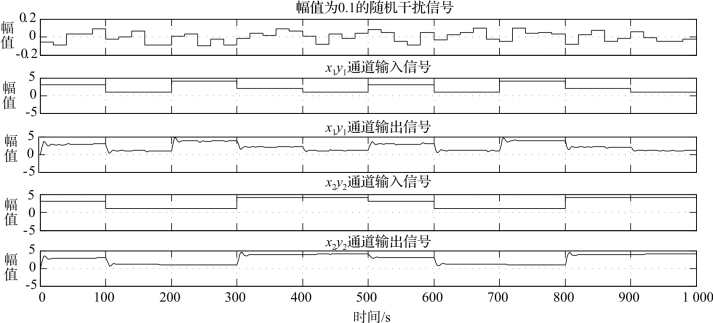
图10-21　解耦后系统的阶跃响应曲线