前馈补偿解耦法是多变量解耦控制中最早使用的一种解耦方法。该方法结构简单，易于实现，效果显著，因此得到了广泛应用。图10-10是一个带前馈补偿解耦器的双变量P规范对象的全解耦系统的方框图。

图10-10　带前馈补偿解耦器的双变量P规范对象的全解耦系统的方框图

如果要实现对Uc2与Y1、Uc1与Y2之间的解耦，根据前馈补偿原理可得

因此，前馈补偿解耦器的传递函数为

利用前馈补偿解耦还可以实现对扰动信号的解耦。图10-11是控制器结合解耦器的前馈补偿全解耦系统的方框图。

如果要实现对扰动量D1和D2的解耦，根据前馈补偿原理得

图10-11　控制器结合解耦器的前馈补偿全解耦系统的方框图

于是得

如果要实现对参考输入量R1（s）、R2（s）和输出量Y1（s）、Y2（s）之间的解耦，则根据前馈补偿原理得

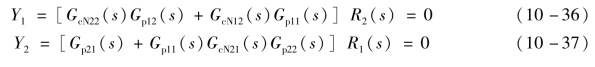(www.daowen.com)

故

比较以上分析结果，不难看出，若对扰动量能实现前馈补偿全解耦，则参考输入与对象输出之间就不能实现解耦。因此，单独采用前馈补偿解耦一般不能同时实现对扰动量及参考输入对输出的解耦。

【例10-3】已知双变量非全耦合系统的方框图如图10-12所示。要求解耦后的闭环传递矩阵为

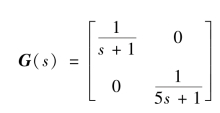
试求控制器结合解耦器的参数。

解：由图10-12可知，系统的闭环传递矩阵为

因此，控制器结合解耦器的传递矩阵为

故

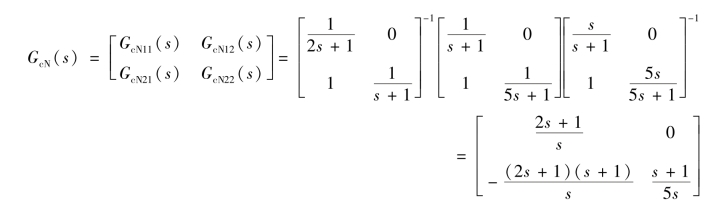
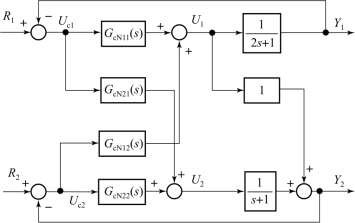
图10-12　双变量非全耦合系统的方框图

由G c N（s）可知，G cN11（s）和G cN22（s）是比例积分控制器，G c N21（s）是比例微分控制器，解耦后，系统等效成2个一阶单回路控制系统，从而实现了被控对象的输出与输入变量之间的解耦。

必须指出的是，对于两变量以上的耦合系统，经过类似的矩阵运算就能求出解耦器的数学模型，但变量越多，解耦器的模型越复杂，解耦器实现的难度就越大。