1.相对增益的定义

相对增益分析法通过利用相对增益矩阵确定过程中每个被控变量相对每个控制变量的响应特性，并以此为依据去设计控制系统。另外，相对增益分析法还可以指出过程关联的程度和类型，以及对回路控制性能的影响。

相对增益分析法作为衡量多变量系统性能尺度的方法，通常称为布里斯托尔-欣斯基方法，用来评价一预先选定的控制变量Uj对一特定的被控变量Yi的影响程度。而且这种影响程度是相对于过程中其他控制变量对该被控变量Yi而言的。

对于一多变量系统，假设Y是包含系统所有被控变量Yi的列向量；U是包含所有控制变量Uj的列向量。为了衡量系统的关联性质首先在所有其他回路均为开环，即所有其他控制变量都保持不变的情况下，得到开环增益矩阵P。这里记作

式中：矩阵P的元素pij的稳态值称为Uj到Yi通道的第一放大系数，是指控制变量Uj改变了ΔUj时，在其余控制变量Uk（k≠j）均不变的情况下，Uj与Yi之间通道的开环增益。显然pij就是除Uj到Yi通道以外，其余通道全部断开时所得到的Uj到Yi通道的稳态增益，pij可表示为

然后，在所有其余回路均闭合，即保持其余被控变量都不变的情况下，找出各通道的开环增益，记作矩阵Q。它的元素qij的稳态值称为Uj与Yi通道的第二放大系数。qij是指利用闭合回路固定其余被控变量Yk（k≠j）时，Uj与Yi之间通道的开环增益。qij可以表示为

pij与qij之比定义为相对增益或相对放大系数λij，λij可表示为

由相对增益λij元素构成的矩阵称为相对增益矩阵Λ，即

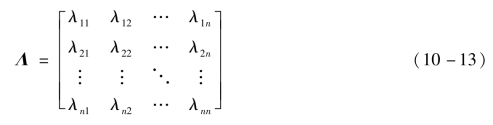
如果在上述2种情况下，开环增益没有变化，即相对增益λij＝1，这就表明由Yi和Uj组成的控制回路与其他回路之间没有关联。这是因为无论其他回路闭合与否都不影响Uj到Yi通道的开环增益。当其他控制变量都保持不变时，Yi不受Uj的影响，那么λij为0，因而就不能用Uj来控制Yi。如果存在某种关联，则Uj的改变不但影响Yi，而且还影响其他被控变量Yk（k≠i）。因此，在确定第二放大系数qij时，使其余回路闭环，被控变量Yk保持不变，则其余的控制变量Uk（k≠j）必然会改变，其结果在2个放大系数之间就会出现差异，即既不是0，也不是1。另外，还有一种极端情况，当式（10-12）中分母趋于0，则其他闭合回路的存在使得Yi不受Uj的影响，此时λ趋于无穷大。关于相对增益具有不同数值时的含义将在下面关于相对增益矩阵的性质中予以讨论。

通常，过程一般都用稳态增益和动态增益来描述，所以相对增益也同样包含这2个分量。然而，在大多数情况下，可以发现稳态增益具有更大的重要性，而且容易求取和处理。

2.相对增益的计算

从相对增益矩阵的定义可以看出，确定相对增益矩阵，关键是计算第一放大系数和第二放大系数。最基本的方法有2种：一种方法是按相对增益的定义对过程的参数表达式进行微分，分别求出第一放大系数和第二放大系数，最后得到相对增益矩阵；另一种方法是先计算第一放大系数，再由第一放大系数直接计算第二放大系数，从而得到相对增益矩阵，即所谓的第二放大系数直接计算法。

1）定义计算法

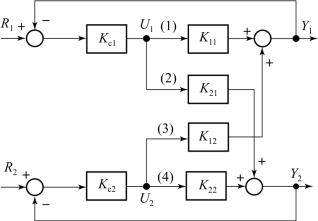
图10-7　双变量稳态耦合系统的方框图

（1）第一放大系数pij的计算。

第一放大系数pij是在其余通道开路且保持Uk（k≠j）恒定的情况下，该通道的稳态增益。下面以图10-7所示的双变量稳态耦合系统为例，说明pij的计算。

如图10-7所示，当计算p11时，可将支路（2）、（3）和（4）断开，或令控制器G c1（s）的增益K c1＝0，改变控制变量U1，求出被控变量Y1，这两者的变化量之比即为p11，不难看出，p11＝K11。实际上，由图10-7所示的双变量稳态耦合系统的方框图可得

根据第一放大系数pij的定义，对式（10-14）求偏导可得

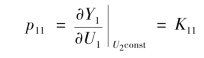
同理可得，p21＝K21，p12＝K12，p22＝K22。

（2）第二放大系数qij的计算。

第二放大系数qij是在其他通道闭合且保持Yk（k≠i）恒定的条件下，该通道的稳态增益。

仍以图10-7双变量稳态耦合系统为例，说明qij的计算。为了确定U1到Y1通道之间的第二放大系数q11，必须保持Y2恒定。利用式（10-14）得Y1与U1和Y2之间的关系表达式为

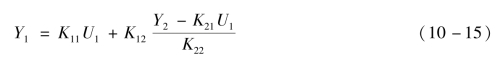
根据第二放大系数qij的定义，对式（10-15）求偏导可得

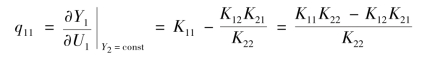
类似地，可求得

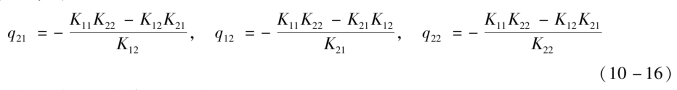
根据相对增益λij的定义，可得

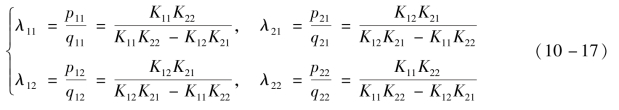
从上述分析可知，第一放大系数pij是比较容易确定的，但第二放大系数qij则要求其他回路开环增益为无穷大的情况才能确定，这不是在任何情况下都能达到的。事实上，由式（10-14）和式（10-16）可看出，第二放大系数qij完全取决于各个第一放大系数pij，这说明有可能由第一放大系数直接求出第二放大系数，从而求得耦合系统的相对增益λij。

2）直接计算法

以图10-7所示双变量耦合系统为例，说明如何由第一放大系数直接求第二放大系数。引入矩阵P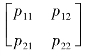＝　，式（10-14）可写成矩阵形式，即

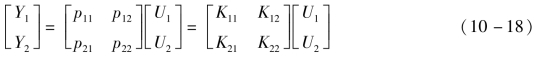
由式（10-18）得

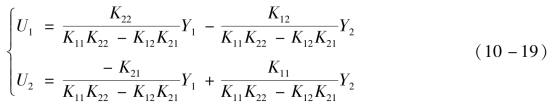
引入矩阵H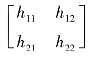＝　，则式（10-19）可写成矩阵形式，即

式中：

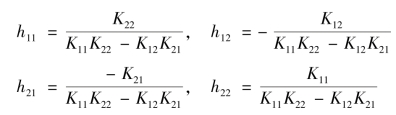
根据第二放大系数的定义，不难看出

由式（10-18）和（10-20）可知(www.daowen.com)

或表示为

根据相对增益的定义，得

由此可见，相对增益可表示为矩阵P中的每个元素与H的转置矩阵中的相应元素的乘积。于是，相对增益矩阵Λ可表示为矩阵P中每个元素与逆矩阵P-1的转置矩阵中相应元素的乘积（点积），即

相对增益的具体计算公式可写为

式中：P ij为矩阵P中元素Pij的代数余子式；det P为矩阵P的行列式。

式（10-26）是由第一放大系数pij计算相对增益λij的一般公式。

3.相对增益矩阵的性质

由式（10-25）可知，相对增益矩阵

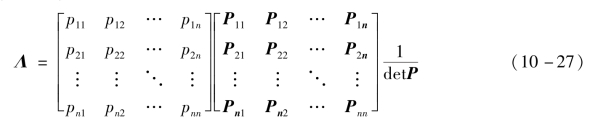
可以证明，矩阵Λ第i行元素之和

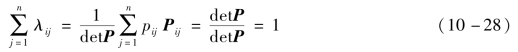
类似地，矩阵Λ第j列元素之和

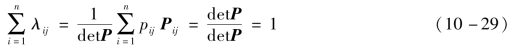
式（10-28）和式（10-29）表明相对增益矩阵中每行元素之和为1，每列元素之和也为1。此结论也同样适用于多变量耦合系统。

【例10-1】如图10-8所示，液体U1、U2在管道中均匀混合后，生成所需成分的混合液。要求对混合液的成分Y1和总流量Y2进行控制，设利用混合液的成分Y1控制总流量Y2的质量百分数为20%，试求被控变量与控制变量之间的正确配对关系。

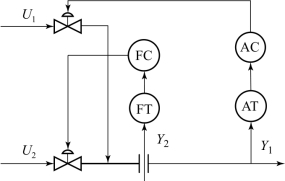
图10-8　液体混合系统

解：由前面的分析可知，要得到正确的变量配对关系，必须首先计算相对增益矩阵。由于此系统的传递函数未知，不能直接用稳态增益求取相对增益。但是，此系统的稳态关系非常清楚，因此可以利用相对增益的定义直接计算。

依题意知，系统的被控变量分别为混合液成分Y1和总流量Y2，控制变量分别为液体U1和U2，满足稳态关系为

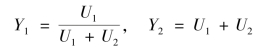
根据定义，先计算U1到Y1通道间的第一放大系数和第二放大系数，得

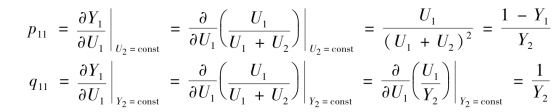
因此，可求得相对增益系数

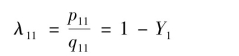
由相对增益矩阵的性质，可得相对增益矩阵

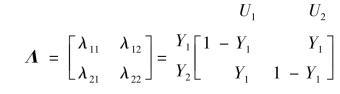
由此可见，系统的相对增益主要取决于混合液成分Y1。因为要选择较大的相对增益的2个变量进行配对，所以，当Y1＝20%时，用控制变量U1控制混合液成分Y1，用控制变量U2控制混合液总流量Y2是比较合理的。

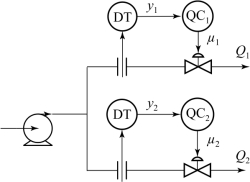
图10-9　并联管道的耦合情况

【例10-2】一母管上有2个并联支路，如图10-9所示。各支路均有流量控制，流经两管的总流量是不变的。假设两管道情况相同，它们的增益也相同，试进行耦合特性分析。

解：当回路开环时，μ1的增加将导致Q1的增加及Q2的减少。所以有

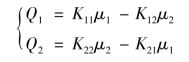
可见，第一放大系数中，有2个为正，2个为负；同时由于管道情况相同，所以有K11＝K22，K12＝K21。它们的相对增益

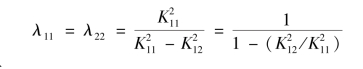
设K11＞K12，则有

由此可见，相对增益λij均落在0～1的范围之外。λ21＝λ12＜0表明，当用μ1控制Q2时，μ2控制Q1回路开、闭环将引起μ1控制Q2回路增益的改变，即当另一个控制回路由开环到闭环时将引起一个不稳定的控制过程，因而不能选择用μ1控制Q2或μ2控制Q1。而λ11＝λ22＞1表明，λ11值越大，则μ1对Q1的控制作用越弱；λ22值越大，则μ2对Q2的控制作用越弱。下面从相对增益的定义也可以说明这个现象：

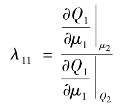
λ11值越大，则表明分母越小，也就是说其他控制回路闭环时，μ1对Q1的控制作用在全部μj（j≠1）的作用中占的比重越小。

上述分析表明，相对增益可以反映如下耦合特性。

（1）如果相对增益λij接近1，如0.8＜λij＜1.2，则表明其他通道对该通道的关联作用很小，可以选为控制通道，同时该通道无须进行解耦系统设计。

（2）如果相对增益λij小于0或接近于0，则表明使用本通道控制器不能得到良好的控制效果。换言之，这个通道的变量选配不恰当，应重新选择。

（3）如果0.3＜λij＜0.7或λij＞1.5，则表明系统中存在着非常严重的耦合，必须进行解耦设计。

（4）无耦合系统的相对增益矩阵必为单位矩阵。反之，系统的相对增益矩阵为单位矩阵时，系统中还可能存在单方向耦合。