1.系统引入前馈控制的原则

如何正确选用前馈控制是设计中首先碰到的问题。当存在反馈控制难以克服的频率高、幅值大、对于被控变量影响大、可测而不可控的扰动或控制系统控制通道纯迟延时间较大而反馈控制又不能得到良好的控制效果时，为了改善和提高系统的控制品质，可以引入前馈控制。一般来说，在系统中引入前馈控制要遵循以下几个原则。

（1）系统中的扰动量是可测不可控的。如果前馈控制所需的扰动量不可测，前馈控制也就无法实现。所谓可测，是指扰动量可以使用检测变送装置在线转化为标准的电信号或气信号。所谓不可控，有2个含义：①指这些扰动难以通过设置单独的反馈控制系统予以稳定，这类扰动在连续生产过程中是经常遇到的；②在某些场合，虽然设置了专门的控制系统来稳定扰动，但由于操作上的需要，往往经常要改变其设定值，也属于不可控的扰动。如果扰动量可控，则可设置独立的控制系统予以克服，也就无须设计较为复杂的前馈控制系统。

（2）系统中的扰动量的变化幅值大、频率高。扰动量幅值变化越大，对被控变量的影响也就越大，系统偏差也越大，因此按扰动量变化设计的前馈控制要比反馈控制更有利。高频扰动对被控对象的影响十分显著，特别是对纯迟延时间小的被控对象，如流量，容易导致系统产生持续振荡。采用前馈控制，可以对扰动量进行同步补偿控制，从而获得较好的控制品质。

（3）在有些工业过程中，由于被控变量难以直接测量实现反馈控制，只能采用前馈控制。例如，连铸二冷配水控制系统，由于二冷区内铸坯表面温度难以在线测量，因而不能采用反馈控制，通常采用基于拉速扰动的二冷水前馈控制方案。

（4）当工艺上要求实现变量间的某种特殊关系，需要通过建立数学模型来实现控制时，可选用前馈控制，这实质上是把扰动量代入已建立的数学模型中去，从模型中求解控制变量，从而消除扰动对被控变量的影响。

2.前馈控制系统的选用原则

当决定选用前馈控制方式后，还需要考虑静态前馈与动态前馈的选择和前馈控制系统结构的选择。

1）静态前馈与动态前馈的选择

在设计过程中可以根据控制通道和扰动通道的时间常数的比值T p/T d来选择前馈控制的类型。通常，当T p/T d＜0.7时，说明扰动通道时间常数大，扰动对系统输出的影响缓慢，有利于反馈控制克服扰动的影响，可不用前馈；当0.7＜T p/T d＜1.3时，可采用静态前馈；当T p/T d＞1.3时，要采用动态前馈。由于动态前馈的结构比静态前馈复杂，而且整定也较麻烦，因此当静态前馈能满足工艺要求时，不必选用动态前馈。如前所述，被控对象的扰动通道和控制通道的时间常数相当时，用静态前馈即可获得满意的控制品质。

2）前馈控制系统结构的选择

前馈控制结构的选择要遵循以下原则。

（1）在满足控制要求的前提下，采用前馈控制的优先性次序为：静态前馈控制、动态前馈控制、前馈-反馈控制和前馈-串级控制。

（2）在实际工业生产过程中，当需要引入前馈控制时，尤其当过程扰动通道与控制通道的纯迟延相差不大时，静态前馈控制可获得较高的控制精度，这时首先考虑采用静态前馈控制。

（3）静态前馈控制只能保证被控变量的静态偏差接近或等于0，不考虑过程扰动通道的时间常数和控制通道的时间常数不同，不能消除过渡过程中所产生的动态偏差。当系统需要严格控制动态偏差时，就要采用动态前馈控制。

（4）当被控对象的扰动较多，或不能精确辨识扰动对被控对象的影响时，可以采用前馈-反馈控制。利用前馈控制对主要扰动进行控制，通过反馈控制抑制由于辨识不精确及其他扰动引起的误差。也就是说，前馈-反馈控制系统将扰动分成2个等级，影响大的扰动采用前馈补偿，保证系统输出不会有过大波动；影响小的扰动允许引起系统输出的偏差，通过反馈进行修正。

（5）当被控对象较复杂，扰动较多，要求控制精度较高时，应采用前馈-串级控制。

（6）在非自衡系统中，不能采用单纯前馈控制，因为开环系统不能改变被控系统的非自平衡性。

3.前馈控制系统的实施

通过对前馈控制系统几种典型结构形式的分析可知，前馈控制器的控制规律取决于被控对象的控制通道和扰动通道的动态特性，而工业对象的特性极为复杂，这就导致了前馈控制规律的形式繁多，按不变性原理实现完全补偿在很多情况下只有理论意义，实际上是做不到的。其原因有2个方面：一方面，被控对象的动态特性很难测得准确，而且一般也具有不可忽视的非线性，特别是在不同负荷下动态特性变化很大，因此用一般的线性补偿器就无法满足不同负荷下的要求；另一方面，写出了补偿器的传递函数并不等于能够实现它，如果G p（s）中包含的纯迟延时间比G d（s）的纯迟延时间大，那就没有实现完全补偿的可能。但从工业应用来看，尤其是使用常规控制仪表组成的控制系统，总是力求控制系统的模式具有一定的通用性，以利于设计、投运和维护。

实际上可以采用前馈控制的大部分过程，其扰动通道和控制通道的传递函数在性质上和数量上都是相近的，通常可用一阶环节或二阶环节来表示。虽然在二者中还可能碰到纯迟延，但是它们的数值一般也比较接近。所以，大多数情况下只需要考虑主要的惯性环节，也就是实现部分补偿，通常采用简单的超前-滞后装置作为动态补偿器就能够满足要求了，其的传递函数为

如超前-滞后环节的输出是c f（t），当输入为单位阶跃时，有(www.daowen.com)

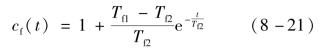
式中：T f1为超前时间；T f2为滞后时间。

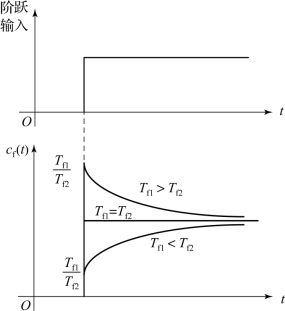
图8-11　超前-滞后环节的阶跃响应曲线

超前-滞后环节的阶跃响应曲线如图8-11所示。当T f1＞T f2时，前馈补偿具有超前特性，适用于控制通道滞后大于扰动通道滞后的被控对象；当T f1＜T f2时，前馈补偿具有滞后特性，适用于控制通道滞后小于扰动通道滞后的被控对象；当T f1＝T f2时，前馈补偿呈现比例特性，即为静态特性。超前-滞后环节的阶跃响应曲线表明，有一瞬时增益为T f1/T f2，而恢复到稳态值的63%所需的时间为T f2。

超前-滞后环节最重要的性能是静态精度。如果在静态下不能准确地复现输入，超前-滞后环节就要降低前馈控制的性能。

利用超前-滞后装置作为动态补偿器进行前馈控制时，当负荷发生变化，补偿器能通过控制通道给过程输入比较多（或比较少）的能量或物质，以改变过程的能量水平。在它的输入和输出函数间的累积面积应该与未经补偿的过程响应曲线中的面积相匹配。如果那样做了，那么响应曲线之净增面积将是0。

式（8-20）所示的超前-滞后前馈补偿器已经成为目前广泛应用的动态前馈补偿模式，在定型的DDZ-Ⅲ型仪表、组合仪表及微型控制器中都有相应的硬件模块，在没有定型仪表的情况下，也可用一些常规仪表组合而成，如用比值器、加法器和一阶惯性环节来实施，如图8-6所示

在前面所示换热器中，应用超前-滞后环节对料液流量改变这一扰动进行动态补偿后，得到的前馈控制系统如图8-12所示。

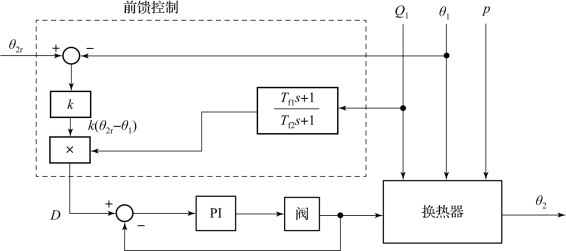
图8-12　换热器前馈控制系统

如图8-13所示，将换热器出口温度在动态前馈控制下的负荷响应曲线与在反馈控制下的负荷响应曲线进行比较。可以看到，当进料流量Q1发生变化时，静态前馈将使出口温度的静态偏差为零，动态偏差也可以补偿到很小的数值，几乎可以说将基本上保持不变，控制效果显然优于反馈控制。应该指出，对入口温度θ1也可以进行动态补偿，只是由于入口温度变化缓慢，通常无须考虑。

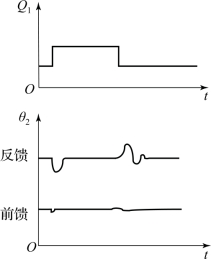
图8-13　换热器前馈和反馈控制下的负荷响应曲线

从以上描述中可以看出前馈控制的优越性：与反馈控制相比，前馈控制不但控制品质好，而且不出现闭环控制系统中所存在的稳定性问题；前馈控制系统中不需要被控变量的测量信号，这种情况有时使得前馈控制成为唯一可行的控制方案。

图8-14为在换热器中实现前馈-反馈控制。当负荷扰动Q1或入口温度θ1变化时，由前馈通道改变蒸汽量D进行控制，除此以外的其他各种扰动的影响及前馈通道补偿不准确带来的偏差，均由反馈控制器来校正。例如，反馈控制器可以用来校正热损失，即要求在所有负荷下都给过程增添一些热量，这好像对前馈控制起了调零的作用；又如，反馈控制器可以校正和控制加热蒸汽压力p的变化等其他扰动的作用。因此，可以说，在前馈-反馈控制系统中，前馈回路和反馈回路在控制过程中起着相辅相成、取长补短的作用。

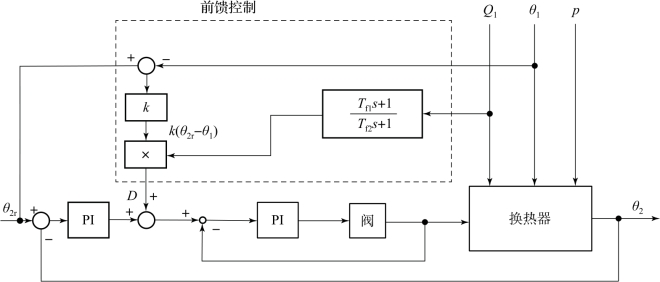
图8-14　换热器前馈-反馈控制系统方案一

图8-15为在换热器上实现前馈-反馈控制的另一种方案。从图中可以看到，由于前馈回路包含了一反馈信号，就能够通过这个反馈信号控制那些未加以测量的扰动。同样，前馈回路也反过来使反馈回路能适应过程增益的变化。从图8-14中换热器在反馈控制下的负荷响应可以看到，随着负荷增加，过渡过程衰减很快；随着负荷减小，过渡过程振幅变大，衰减变慢，这表明过程的增益与料液流量成反比，过程呈现出非线性特性。若使反馈控制器的增益与流量成正比，则将弥补此非线性特性，使系统增益不随负荷变化。图8-15中的方案恰好能做到这一点。反馈回路把θ2作为输入信号，把D作为输出。但是在回路的内部，反馈控制器的输出值要先减去θ1，然后再乘以Q1。其中，减法是线性运算，而乘法却是非线性运算，它使反馈回路的开环增益与流量成正比，正好抵消了换热器本身增益的变化。

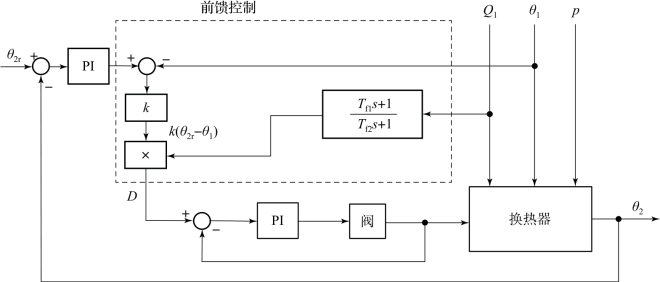
图8-15　换热器前馈-反馈控制系统方案二

由上例可以看到，前馈控制和反馈控制之间，前馈是快的、有智能的和敏感的，但是它不准确；反馈是慢的，但却是准确的，而且在负荷条件不明的情况下还有控制能力。这2种回路的相互补充，相互适应构成了十分有效的控制方案。在实践中，前馈-反馈控制系统正越来越多地得到采用，而且得到了十分显著的控制效果。