二步整定法虽然比逐步逼近法简便得多，但仍然要分二步进行整定，要寻求2个4∶1的衰减振荡过程，因而仍比较麻烦。在采用二步整定法整定参数的实践中，对二步整定法反复进行总结、简化，从而得到了一步整定法。所谓一步整定法，就是根据经验先确定副控制器的比例带，然后按照简单控制系统的整定方法整定主控制器的参数，一步整定法的整定准确性虽然比二步整定法低一些，但由于方法更简便，易于操作和掌握，因而在工程上得到了广泛的应用。

一步整定法是在工程实践中被发现的，对于串级控制系统，在纯比例控制的情况下，要得到主变量的4∶1衰减振荡过程，主、副控制器的放大系数K c1、K c2可以有好几组搭配，其相互关系近似满足K c1 K c2＝K s（常数），表7-2所示的实验数据可以说明这一点。

表7-2　主、副控制器放大系数匹配实验数据

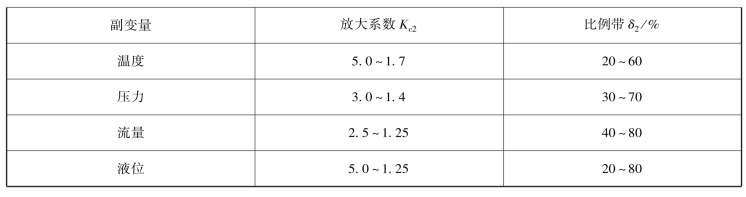
当采用1～3组整定参数时，主变量均可得到4∶1衰减振荡过程，且过渡过程时间均在9 min左右，而K s一般为3.30。这说明主、副控制器的放大系数可以在一定范围内任意匹配，而控制效果基本相同。这样，就可以依据经验先将副控制器的比例带确定一个数值，然后按一般简单控制系统的参数整定方法整定主控制器的参数。虽然副控制器按经验设置的比例带不一定很合适，但可以通过调整主控制器的比例带进行补偿，使主变量最终得到4∶1的衰减振荡过程。对副控制器的比例带δ2或放大系数K c2的估计，可利用表7-3中的经验数值确定一范围。

一步整定法的具体步骤如下。

（1）由表7-3选择副控制器的比例带，使副回路按比例控制运行。

（2）将系统投入串级控制状态运行，按简单控制系统参数整定的方法对主控制器进行参数整定，再通过参数调整，使主变量的控制品质达到满意控制效果。

表7-3　副控制器比例带取值范围

【例7-2】某隧道窑系统，构成以烧成带温度为主变量，燃烧室温度为副变量的串级控制系统。假设主、副对象的传递函数分别为

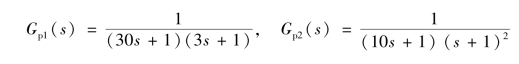
试分析串级控制系统对二次扰动的抗扰动能力，并与采用等效单回路控制时的抗扰动能力进行比对分析。(www.daowen.com)

解：（1）首先分析采用串级控制时的情况，在t＝50 s时，在副回路施加一宽度为10 s、幅值为2的脉冲扰动。Simulink仿真框图如图7-14所示。

图7-14　串级控制系统仿真框图

（2）对主、副控制器采用上述整定方法进行整定，也可以采用MATLAB中的NCD Output模块进行PID参数优化计算，最终确定串级控制系统的控制器参数为：主控制器中K c1＝6.2、T i1＝33.7、T d1＝0.7，副控制器中K c2＝12.0。

图7-15　串级控制系统对进入副回路扰动的抗干扰阶跃响应曲线

（3）利用Simulink的Simulation→Simulation Parameters命令，将仿真的停止时间设置为100，其余参数采用默认值。启动仿真，可得到串级控制对进入副回路扰动的抗扰动阶跃响应曲线，如图7-15所示。

同样，在图7-16所示的等效单回路控制系统中加入相同的扰动，可得到如图7-17所示的阶跃响应曲线。同样采用NCD Output模块进行PID参数优化计算，此时整定的PID参数为：K c＝10.4、T i＝81.7、T d＝6.9。

对比图7-15和图7-17，可得出如下结论：在相同的扰动作用下，串级控制系统的超调量明显比等效的单回路控制系统要小得多，可见串级控制系统对二次扰动有很好的抑制能力。

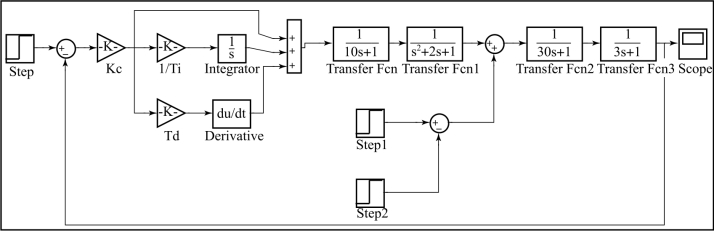
图7-16　加入扰动的等效单回路控制系统仿真框图

图7-17　加入扰动的等效单回路控制系统的阶跃响应曲线