为了避免串级控制系统发生共振，应使主、副对象的工作频率匹配。

1.产生共振的原因

对于二阶系统，当系统阻尼比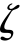＜0.707时，系统的幅频特性呈现一个峰值，如果外界扰动信号的频率等于谐振频率，则系统进入谐振，或称为共振，这是二阶系统所具有的特性。

对于二阶系统，其传递函数为

式中：ωn为系统的自然频率；为系统的阻尼比。

由自动控制理论可知，系统的工作频率ωd和谐振频率ωr与自然频率ωn、阻尼比之间的关系为

系统的幅频特性M（ω）为

其关系曲线如图7-10所示，从图中可以看出，除了当ω＝ωr时有一峰值点外，二阶系统还有一个增幅区域，即在谐振频率的一定区域内，系统的幅值有明显的增大，可以称这个区域为广义共振区。这个共振区的频率范围是

也就是说，当外界扰动频率在这个区域之外时，系统增幅是很小的，甚至没有增幅。式（7-10）是二阶振荡系统的广义共振频率条件。

在串级控制系统中，由于主、副回路是两个相互独立又紧密相关的回路。如果系统受到扰动作用从副回路看，主控制器无时无刻不向副回路输送信号，相当于副回路一直受到从主回路来的连续性扰动，这个扰动信号的频率就是主回路的工作频率ωd1；从主回路看，副回路的输出对主回路也相当于是一个持续作用的扰动，这个扰动信号的频率就是副回路的工作频率ωd2。如果主、副回路的工作频率很接近，彼此都落入了对方的广义共振区，那么在受到某种扰动作用时，主变量的变化进入副回路时会引起副变量振幅的增加，而副变量的变化传送到主回路后，又迫使主变量的变化幅度增加，如此循环往复，就会使主、副变量长时间地大幅度波动，这就是所谓串级控制系统的共振现象。一旦发生了共振，系统就失去控制，使控制品质恶化，如不及时处理，甚至可能导致生产事故，引起严重后果。为了避免这种现象发生，在设计时必须将主、副回路的工作频率错开。

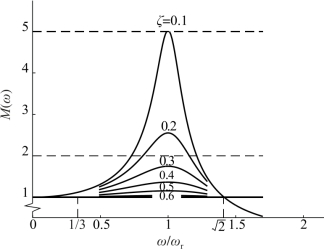
图7-10　二阶振荡系统的幅频特性(www.daowen.com)

2.产生共振的条件

假定串级控制系统的主、副回路都是二阶系统，而且都按4∶1衰减曲线的要求进行整定，即系统阻尼比＝0.216。从副回路看，主控制器一直向副回路输送信号，相当于副回路一直受到从主回路来的频率为ωd1的连续性扰动信号。如果要避免副回路进入共振区，则主回路的工作频率ωd1与副回路的共振频率ωr2必须满足

由式（7-8）知，在ζ＝0.216时，ωr与ωd十分接近。对于副回路，则有ωr2≈ωd2，则式（7-11）可以写成

同样，从主回路看，副回路的输出对主回路也相当于是频率为ωd2的连续性扰动。为了避免主回路进入共振区，同理可得

考虑到副回路通常是快速回路，其工作频率总是高于主回路工作频率，为了保证主、副回路均避免进入共振区，从式（7-12）和式（7-13）可以得到的条件是

为确保串级控制系统不受共振现象的威胁，一般取

由于系统的工作频率与时间常数近似成反比关系，所以在选择副变量时，应考虑主、副回路时间常数的匹配关系，通常取

上述结论虽然是在假定主、副回路均是二阶系统的前提下得到的，但也不失其一般性。原因是系统经过整定后，总有一对起主导作用的极点，整个回路的工作频率由它们决定，即可以把这个系统看作近似二阶振荡系统。

当然，为了满足式（7-15），使主回路的时间常数为3～10倍于副回路的时间常数，除了在副回路的设计中加以考虑外，还与主、副控制器的整定参数有关。

另外，实际应用中T1、T2究竟取多大为好，应根据具体对象的情况和控制系统要达到的目的而定。如果串级控制系统的目的是克服对象的主要扰动，那么副回路的时间常数小一点为好，只要将主要扰动纳入副回路就行了；如果串级控制系统的目的是克服对象时间常数过大和滞后严重，以便改善对象特性，那么副回路的时间常数可适当大一些；如果想利用串级控制系统克服对象的非线性，那么主、副回路的时间常数最好相差大一些。