与模拟PID控制器参数整定相同，数字PID控制器参数整定就是选择算式中K c、T i和T d的值，使数字系统输出响应y（t）满足某种选定的准则，可分为以下2类。

（1）简单近似准则，如系统输出响应的超调量、衰减比、上升时间和调节时间等准则。其中，4∶1衰减比通常被认为是最佳的综合准则，它既保证系统的稳定性又照顾系统的快速性。

（2）精确准则，如各类误差的积分准则。对于离散系统可提出各种积分准则为

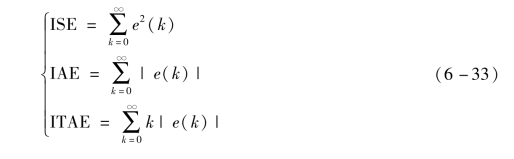
PID控制算法的所谓“最佳参数”就是根据系统在规定的输入下的输出响应能使式（6-33）中某一准则取最小值的参数。显然，不同准则所得的最佳参数值也不同。经对比研究表明，以误差积分准则为基础的各种参数整定方法较好，尤其是被控对象τ／T比值较大的情况。而在各类积分准则中，又以ITAE为最佳。

与模拟控制器参数整定不同，在整定数字PID控制算法各参数的同时，必须考虑采样周期T0的影响。这是因为数字系统的控制品质不仅取决于对象的动态特性和PID算法的整定参数（K c、T i和T d），而且与采样周期T0的大小有关。下面介绍目前工程上常用的几种数字PID参数整定方法。

1.采样周期的确定

一般说来，计算机控制系统的控制性能会随着采样加快而得到改善，但同时对控制设备软硬件的要求也会更高。所以，在系统性能与成本之间往往需要进行一定的折中。换句话说，要在保证控制性能要求的条件下，来合理选择采样周期。采样周期的选择原则：

（1）提高控制品质，T0可取小些；

（2）减小超调量，T0可取大些；

（3）减小调节时间，T0可取小些；

（4）数字PID控制要把T0、T i、T d结合在一起考虑。

2.扩充响应曲线法

鉴于在大部分数字控制系统中各控制回路的时间常数比采样周期大得多，因而可以把模拟控制器动态特性参数整定方法推广应用来整定数字P1D算法参数。只要用一个纯迟延环节等效数字系统中的采样-保持器，并引入等效纯迟延时间的概念，那么所有基于对象响应曲线的模拟控制器参数整定方法，如齐格勒-尼科尔斯（Z-N）、柯恩-库恩（C-C）以及基于误差积分的参数整定公式，均可直接用来计算数字PID算法中K c、T i、T d等参数值。注意，公式中被控对象的延迟时间τ要用等效延迟时间τe代替，此处τe定义为被控对象的τ与采样周期T0的一半之和，即

式中：T0/2是考虑了数字系统中采样-保持器环节引起的滞后。

扩充响应曲线法是开环整定方法。与模拟控制器动态特性参数法类似，预先测得广义被控对象的阶跃响应曲线，并以带纯迟延τ和时间常数T的一阶惯性环节近似，然后从曲线求得τ和T，具体步骤如下。

（1）如果已知系统的动态特性曲线，那么就可以把模拟控制器动态特性参数法整定方法推广到数字控制系统，采用扩充响应曲线法进行整定。

（2）在应用Z-N公式和C-C公式时，被控对象的延迟时间τ要用等效延迟时间τe代替。

（3）选择控制度。所谓控制度，就是以模拟控制器为基准，将数字控制系统的控制效果与模拟控制器的控制效果相比较，表示二者控制品质的差异程度，其评价函数通常采用误差平方积分，表示为

对于模拟系统，其误差平方积分可按记录曲线上的图形面积计算；而对于DDC系统，其误差平方积分可用计算机直接计算。通常情况下，当控制度为1.05时，表示数字控制系统与模拟系统控制效果相当；当控制度为2.00时，控制品质差一倍。需要注意的是，在选择控制度时，并不是越小越好，要根据实际系统硬件配置和采样周期的大小等因素来选择，否则确定的PID参数在投入运行后，控制系统的性能反而会变差。

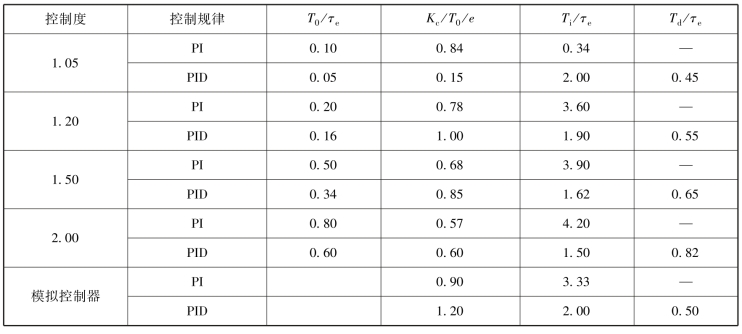
（4）根据选择的控制度和求得的τe、T和K值，查表6-2即可求出控制器的T0、K c、T i、T d。

（5）由于被控对象的特性不同，经验公式求得的控制器参数整定不一定都能获得满意的结果，需针对具体系统在实际运行过程中作在线修正。

表6-2　扩充响应曲线法整定参数表(www.daowen.com)

3.扩充临界比例带法

扩充临界比例带法是简易工程参数整定方法，也是基于系统临界振荡参数的闭环整定方法。这种方法实质上是模拟控制器中采用的稳定边界法的推广，用来整定离散PID算法中的T0、K c、T i和T d参数，具体步骤如下。

（1）选择一个足够短的采样周期T min，如带有纯迟延的系统其采样周期取纯迟延时间的1/10以下。

（2）求出临界比例带δcr和临界振荡周期T cr。具体方法是，将上述的采样周期T min输入到计算机控制系统，并只采用比例控制，逐渐增大比例系数K c，直到系统产生等幅振荡。此时的比例系数即为临界比例带δcr，相应的振荡周期称为临界振荡周期T cr。

（3）选择控制度。

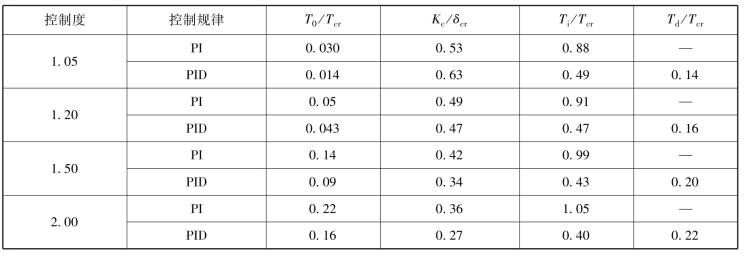
（4）根据控制度，查表6-3求出参数。

（5）将参数加到系统中调试运行。

表6-3　扩充临界比例带法整定参数表

4.归一参数整定法

以上两种方法用于被控对象是一阶滞后环节时有些麻烦。1974年，Roberts提出一种简化扩充临界比例带整定法。由于该方法只需整定一个参数即可，故称其为归一参数整定法。

PID归一参数整定法的指导思想：根据经验数据，对多变量、相互耦合较强的系数，人为地设定“约束条件”，以减少变量的个数，达到减少整定参数数目、简易、快速整定参数之目的。

已知增量型PID控制算法的表达式为

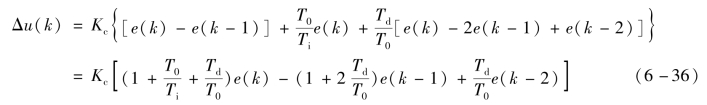
根据经验规律，可以设置各个时间参数之间的关系，即“约束条件”，设

式中：T cr为纯比例下的临界振荡周期。

将式（3-37）代入式（6-36）化简得

式（6-38）即为归一化参数整定法的表达式。式中参数K c通过实验对其调整，便会达到满意的控制效果。

参数K c的实验确定方法：

（1）给一阶跃输入，记录输出曲线，如速度、压力、温度等变化曲线，调整参数K c值，使曲线尽量接近理想曲线；

（2）实际运行，再进一步调整参数K c值，使实际控制效果达到最佳。

应当指出，第5章中有关控制器参数自整定原理同样适用于数字系统PID算法中参数的整定。事实上，只有应用了计算机以后，控制器参数的自整定才成为可能。当今DCS系统和一些PLC控制器一般都配备参数自整定功能。