基本PID控制是基于偏差来进行调节的，以实现过程的闭环控制。引起偏差的因素主要来自两个方面：一是过程扰动；二是设定值变化。闭环系统对于过程扰动以及设定值变化扰动的响应特性反映了系统的2个不同侧面（具有不同的闭环传递函数）。采用同一组PID控制器参数往往难以保证2个方面的特性都十分理想。为适应不同被控对象和系统的要求，改善系统控制品质，可在标准PID控制算法基础上进行某些改进，形成非标准的PID控制算法，如不完全微分PID算法，微分先行PID算法，带不灵敏区的PID算法，积分分离PID算法等。在实际应用中，一些常用的控制器（如PLC、DCS控制系统等）会提供标准类型的PID库函数，非常方便编程调用，但对于改进算法往往需要自己编程。下面介绍几种具有代表性的PID改进算法及相应的程序流程图。

1.不完全微分PID算法

标准的PID算法的缺点是对具有高频扰动的生产过程，微分作用响应过于灵敏，容易引起控制过程振荡，降低控制品质。尤其在数字控制系统中，计算机对每个控制回路的输出时间是短暂的，而驱动执行器动作却需要一定时间。如果输出较大，在短暂时间内执行器达不到应有的开度，会使输出失真。为克服这一弱点，同时又要使微分作用有效，可在PID控制器输出串联一阶惯性环节，如图6-8所示。

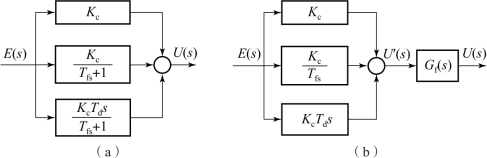
图6-8　不完全微分PID控制器

这就形成了两类不完全微分PID控制器，下面以图6-8（b）为例来说明不完全微分PID控制器输出算式的推导过程，即

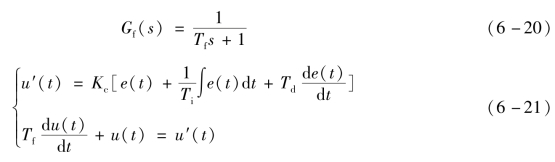
所以

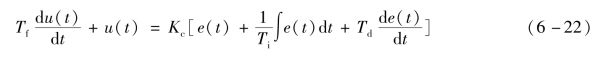
将式（6-22）数字化，可得不完全微分位置型控制算法表达式为

式中：α＝T f/（T0＋T f），T f为惯性时间常数，通过调整其值的大小改变惯性环节的作用效果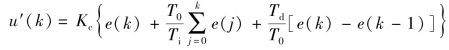；；α为介于0～1之间的系数。

与标准PID一样，不完全微分也有增量型控制算法表达式，即

式中：

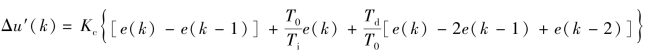
相应的不完全微分速度型控制算法表达式为

式中：

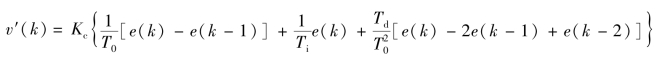
图6-8（b）所示的位置型不完全微分PID算法的程序流程如图6-9所示。

图6-10分别表示标准PID算法和不完全微分PID算法在单位阶跃响应输入时，输出的控制作用。由图可见，标准PID算法中的微分作用只在第一个采样周期起作用，而且作用很强。反之，不完全微分PID算法的输出在较长时间内保持微分作用，且作用强度有明显的缓和，可获得较好的控制效果。

2.微分先行PID算法

为了避免给定值阶跃变化，偏差突变，微分引起控制变量大幅度变化等给控制带来冲击（超调量过大或调节阀动作剧烈）。考虑到通常情况下被控变量的变化总是比较和缓，因此微分先行PID算法就只对测量值y（t）微分，而不对偏差e（t）微分，也就是说对给定值r（t）无微分作用。这样在调整设定值时，控制器的输出就不会产生剧烈的跳变，也就避免了给定值变化给系统造成的冲击。图6-11为微分先行PID控制器结构方框图。

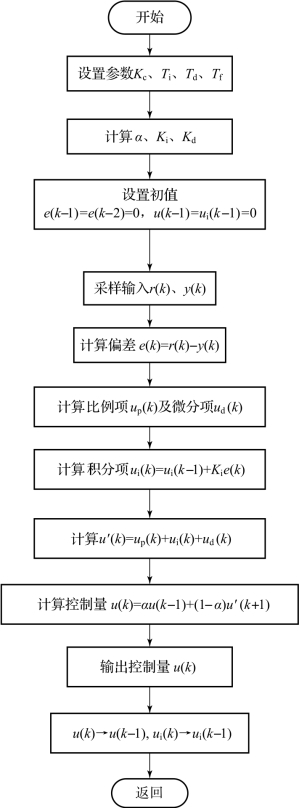
图6-9　位置型不完全微分PID算法的程序流程

增量型PID控制算法表达式的微分项为

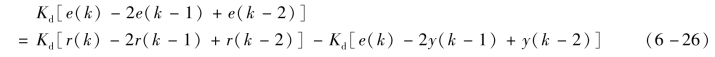
如果只对被控变量微分，那么式（6-17）的增量型PID控制算法表达式变为

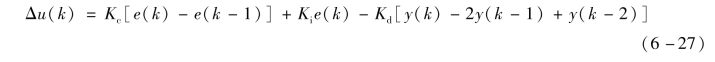
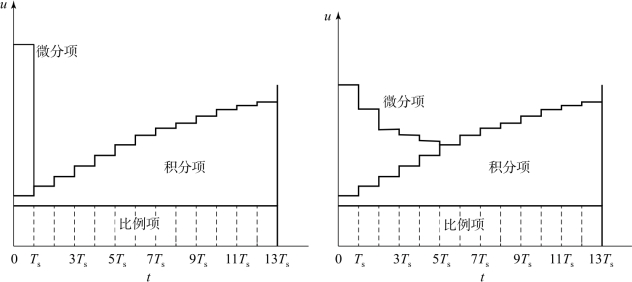
图6-10　标准PID、不完全微分PID算法输出响应

（a）标准PID算法输出响应；（b）不完全微分PID算法输出响应

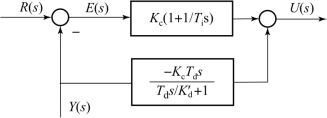
图6-11　微分先行PID控制器结构方框图

由式（6-27）可知，微分先行PID控制流程与标准PID类似，只是计算微分项时，由e（i）变成了-y（i），其中i可为k，k-1，k-2。

【例6-1】设被控对象为具有时滞的惯性环节，其传递函数为，系统采样周期为20 s。输入信号为带有高频扰动的方波信号y d＝sin（0.000 5πt）2＋0.05 sin（0.03πt）。试比较微分先行PID算法和标准PID算法的控制效果。

解：首先通过以下MATLAB代码求取仿真输入信号simin：(www.daowen.com)

选取K p＝0.56，K i＝0.008 1，K d＝30。通过Simulink模块实现微分先行PID算法，如图6-12所示，设置Gain为0.56，Gain1为0.008 1，Gain2为-30。方波响应结果如图6-13所示。

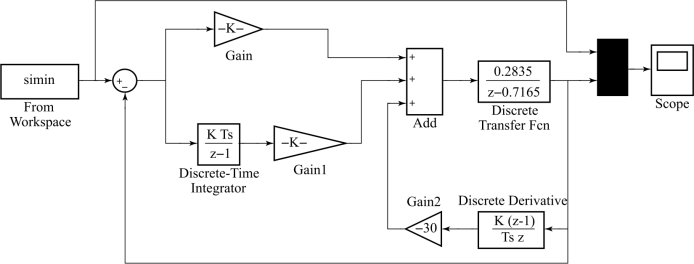
图6-12　微分先行PID算法的Simulink仿真图

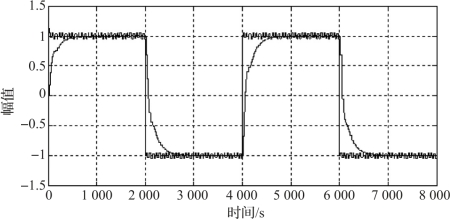
图6-13　微分先行PID算法的方波响应

同样通过Simulink模块实现标准PID算法，其参数均与微分先行PID算法的参数相同。标准PID算法的方波响应如图6-14所示。

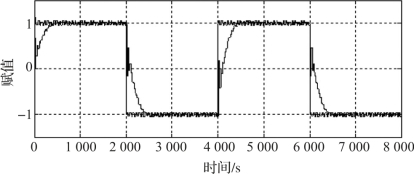
图6-14　标准PID算法的方波响应

由仿真结果可以看出，对于给定值频繁升降的场合，引入微分先行后，可以避免给定值升降所引起的系统振荡，明显地改善系统的动态特性。

3.带不灵敏区的PID算法

某些过程控制系统，并不要求液位准确控制在给定值，而是允许在规定范围内变化。在这种情况下，为避免调节阀频繁运动以及因此所引起的系统振荡，可采用带不灵敏区（死区）的PID算法，人为地设置一个不灵敏区域B，当偏差e（t）的绝对值小于B时，其控制输出不变，否则使其输出为正常输出。即

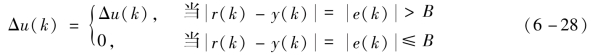
式中：B为不灵敏区宽度，其数值根据被控对象由实验确定。B值太小，则调节阀动作频繁；B值太大，则系统迟缓；B＝0，则为标准PID算法。

式（6-28）表明，当偏差绝对值｜e（k）｜≤B时，输出增量为0。当｜e（k）｜＞B时，输出Δu（k）为e（k）经PID运算后的结果。

带不灵敏区的PID算法的程序流程如图6-15所示。

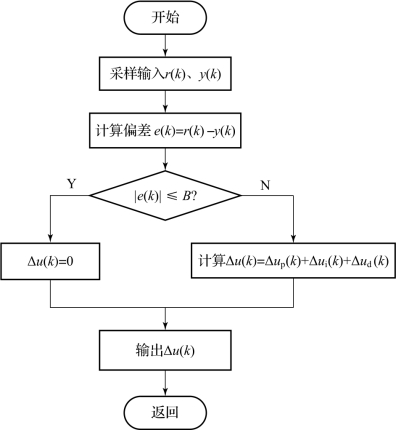
图6-15　带不灵敏区的PID算法的程序流程

4.积分分离PID算法

采用标准PID算法的数字系统在开工、停工或给定值大幅度升降时，由于短时间内出现的大偏差，加上系统本身的迟延，在积分项的作用下，将引起系统产生过大的超调量或不停地振荡。为此，可采取积分分离对策，也就是在起始阶段对被控变量开始跟踪，系统偏差较大时，暂时取消积分作用，一旦被控变量接近新给定值，偏差小于某一设定值A时，投入积分作用。积分分离PID算法表达式为

值得注意的是，为保证引入积分作用后系统的稳定性不变，在引入积分作用的同时，比例增益K c应作相应变化（K c应减小），这可以在PID算法编程时加以考虑。另外，在设定A值时应保证设置合理，否则会因A值太小而使得系统的积分控制不能引入。积分分离PID算法的程序流程如图6-16所示。

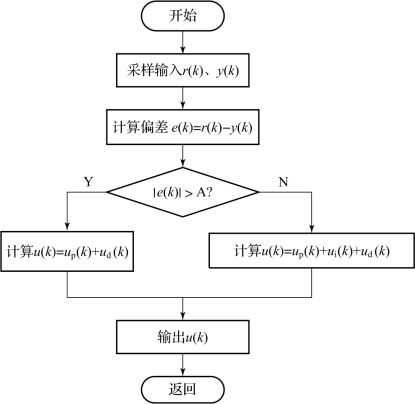
图6-16　积分分离PID算法的程序流程

5.变速积分PID算法

控制系统对积分项的要求是，系统偏差大时积分作用应减弱甚至全无，而在偏差小时应加强。否则，积分系数取大了会产生超调，甚至积分饱和，取小了又迟迟不能消除余差。因此，如何根据系统偏差大小改变积分速度，对于提高系统品质是很重要的。采用变速积分PID算法可以较好地解决这一问题。积分分离PID算法是它的简化算法。

变速积分PID算法的基本思想是设法改变积分项的累加速度，使其与偏差的大小相对应，即偏差越大，积分越慢；偏差越小，积分越快。

为此，设一系数f［e（k）］，它是偏差e（k）的函数。当｜e（k）｜增大时，f［e（k）］减小；反之，f［e（k）］增大。每次采样后，用f［e（k）］乘以e（k），再进行累加，即

式中：u i（k）为变速积分项的输出值。

系数f［e（k）］与｜e（k）｜的关系可以是线性或非线性的，通常可设为

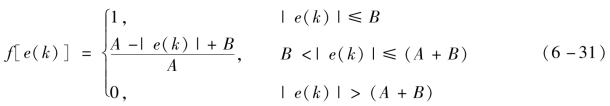
式中：A和B根据被控对象的特点和系统的性能指标要求来确定。

将u l（k）代入位置型PID控制算法表达式，得到变速积分PID算法表达式为

变速积分PID算法的程序流程如图6-17所示。

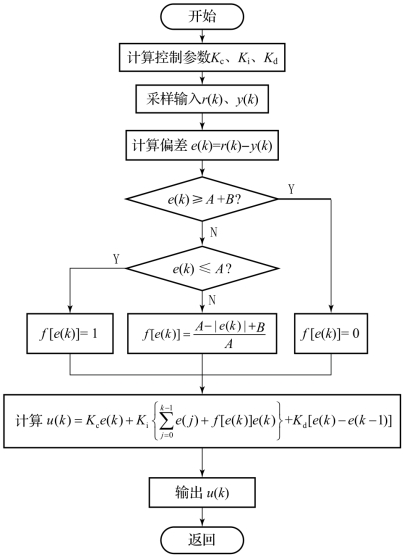
图6-17　变速积分PID算法的程序流程