为了抑制进入数字系统的信号中可能侵入的各种频率的扰动，通常在模入部件的入口处设置模拟RC滤波器。这种滤波器能有效地抑制高频扰动，但对低频扰动的抑制效果不佳。而数字滤波对此类扰动（包括周期性和脉冲性扰动）却是一种有效的方法。

所谓数字滤波就是通过一定的计算程序对采样信号进行平滑加工，消除或削减各种扰动和噪声，以提高信号的有效性。其与模拟滤波相比有下列优点：不增加任何硬件设备，只需在程序进入数据处理和控制算法之前，附加一段数字滤波程序；稳定性高；不存在阻抗匹配问题，可供多个通道共用；不像模拟滤波受电容容量的影响，只能对高频扰动进行滤波；使用灵活、方便，可视需要选择不同滤波方法或改变滤波器参数。正因为上述这些优点，数字滤波在计算机控制系统中得到广泛应用。下面介绍几种常用的数字滤波方法。

1.程序判断滤波

随机扰动、误检测或者变送器可靠性不良会引起采样信号大幅度跳码，导致计算机系统误动作。对这类扰动，可采用程序判断滤波除去错误信号。程序判断滤波根据滤波方法的不同，可分为限幅滤波和限速滤波两种。

1）限幅滤波

限幅滤波就是把两次相邻的采样值进行相减，将其增量（以绝对值表示）与两次采样允许的最大差值Δy比较，如果小于或等于Δy，则取本次采样值；如果大于Δy，则仍取上次采样值作为本次采样值。具体可表示为

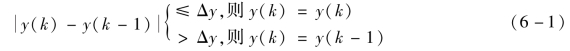
式中：y（k）为第k次采样值；y（k-1）为第（k-1）次采样值。

Δy是可选的常数，正确选择该值是应用本方法的关键，Δy值的选择视被控变量的变化速度而定。

2）限速滤波

限速滤波最多可用3次采样值来决定采样结果，设顺序采样时刻为t1，t2，t3，采集值分别为y1，y2，y3，若

限速滤波适用于温度、液位等变化比较缓慢的信号。

2.递推平均滤波（算术平均滤波）

某些过程参数如流量、压力或沸腾状液位等，其变送器的输出总是在某一数值上下波动，如图6-4所示。

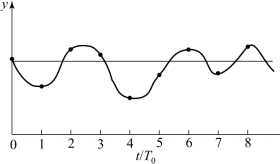
图6-4　算术平均值图

图6-4中的黑点表示各采样时刻读入的数值。显然，这类信号会导致控制算式输出紊乱，调节阀动作频繁，从而影响其使用寿命，降低系统的控制品质。为此，采用递推平均滤波，以其算术平均值作为计算机的输入信号，即

式中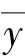：（k）为第k次采用的N项递推平均值；y（k-i）为往前递推的第i次的采样值；N为递推平均项数。

这种方法适用于带周期性噪声的采样信号的平滑加工。N值的大小决定了采样平均值的平滑度和反应的灵敏度。N值增大，信号平滑度提高，但对信号变化反应的灵敏度降低，占用机时长，实际上可根据不同N值下递推平均的输出响应来决定。通常，流量取12项采样信号平均，压力取4项平均，而温度一般比较平稳，可少取几项甚至不加以平均。此方法的缺点是N较大时，占用机时较长，效率低。

3.加权递推平均滤波（滑动平均值法）

式（6-4）中的N项递推平均值，其计算结果对N次采样值的比重是均等的。为了提高滤波效果，可先将各采样值取不同的比例然后相加，这就是加权递推平均滤波。N项加权平均值为

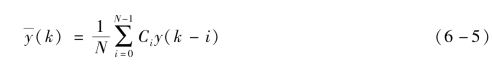
式中：C0，C1，…，CN-1均为加权系数，并满足

Ci值根据具体情况而定，一般采用次数愈靠后，取值愈大，这样可以增加新采样值在平均值中的比重。(www.daowen.com)

本方法适用于纯迟延较大的被控对象。如果采用4项加权递推平均滤波，加权系数的计算式为

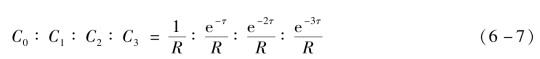
式中：R＝1＋e-τ＋e-2τ＋e-3τ；τ为被控对象的纯迟延时间。

4.中值滤波

中值滤波是在3个采样周期内，连续采样3个数据x1、x2、x3，从中选择一大小居中的数据作为采样结果，用算式表示为：若x1＜x2＜x3，则x2为采样结果。

中值滤波对于去掉偶然因素引起的波动或传感器不稳定而造成的误差所引起的脉冲扰动比较有效，对缓慢变化的过程变量的滤波效果比较好，但对快速变化的过程变量（如流量），则不宜采用。中值滤波对于采样点多于3个的情况不宜采用。

5.一阶惯性滤波

上述几种滤波方法基本均属于稳态滤波，适用于响应过程较快的参数，如压力、流量等。对于慢变化过程，为提高滤波效果，可采用动态滤波方法，如一阶惯性滤波方法。

一阶惯性滤波环节的传递函数为

式中：T f为滤波时间常数，T f＝RC。

式（6-8）通过差分变换可得

式中：y（k-1）为滤波器前一周期的输出值；α＝T f/（T f＋T0），称为滤波平滑系数。

由于T0远小于T f，因此是惯性环节。此外，上式中α也可以采用。

通常惯性滤波器的采样周期远小于滤波器的时间常数，也就是输入信号的频率快，而滤波器的时间常数相对较大。

当T0≪T f时，α≈1，则采样信号偶然跳变引起的影响小，对信号响应迟缓。因此，应根据实际情况，选择α值。

6.复合数字滤波

为了进一步提高滤波效果，有时可以把两种或两种以上不同滤波功能的数字滤波器组合起来，组成复合数字滤波器，或称多级数字滤波器。例如，前面介绍的算术平均滤波只能对周期性的脉动采样值进行平滑处理，无法消除随机的脉冲扰动，但中值滤波却可以解决这个问题。因此，可以将二者组合起来，形成多功能的复合数字滤波，即把采样值先按从小到大的顺序排列起来，然后将最大值和最小值去掉，再把余下的部分求和并取平均值。该方法兼容了算术平均滤波和中值滤波的优点，当采样点数不多时，它的优点不够明显，但在快、慢速系统中，它却都能削弱扰动，提高控制品质。

7.各种数字滤波性能的比较

以上介绍的数字滤波方法各有其特点，可以根据具体的测量参数进行合理的选用。

1）滤波效果

一般来说，对于变化比较慢的参数，如温度，可选用程序判断滤波或一阶惯性滤波方法。对那些变化比较快的脉冲参数（如压力、流量），则可选择算术平均滤波或加权递推平均滤波方法，至于要求比较高的系统，需要用复合数字滤波方法。在算术平均滤波或加权递推平均滤波中，其滤波效果与所选择的采样次数n有关，n越大，则滤波效果越好，但花费的时间也越长。高通或低通滤波是比较特殊的滤波程序，使用时一定要根据参数特点选用。

2）滤波时间

在考虑滤波效果的前提下，应尽量采用执行时间比较短的滤波方法，若计算时间允许，则采用效果更好的复合数字滤波方法。

要注意的是，数字滤波在热工或化工过程控制系统中并非一定需要，要根据具体情况，经过分析、实验加以选用。不适当的数字滤波反而会降低控制效果，甚至导致系统失控。