数字控制系统由于仅在采样时刻的数值才与模拟控制系统的数值完全相等，那么数字控制系统是否能够完全反映模拟控制系统的情况，或者说数字控制系统是否是模拟控制系统的真实再现呢？要回答这个问题，就涉及与数字控制系统相关的一些基础理论知识。完备的相关知识可以从控制理论、信号处理等相关课程内获得，本节仅介绍其中最重要和最基础的一些知识。

1.采样定理

采样定理（Nyquist-Shannon sampling theorem）是由Nyquist H、和Shannon C.E.分别于1928年和1949年提出的。采样定理指出，在一定的条件下一个连续的时间信号完全可由该信号在等时间间隔点的样本值来表示，并且可以用这些样本值把该信号全部恢复出来。由此可知，只要数字控制系统满足一定的条件，它与原连续系统是完全等价的。因此，采样定理也就成为数字系统的一个基本原理。

采样定理的内容为：若连续信号x（t）是有限带宽的，其频谱的最高频率为f x，对于x（t）以采样时间T0进行等间隔采样，获得采样结果x（nT0），若保证采样频率f s＝1/T0≥2f x，那么，可由x（nT0）完全恢复x（t），即x（nT0）保留了x（t）中的全部信息。显然，要满足采样定理，必须满足两个条件：首先，被采样信号是有限带宽的，否则不可能到其两倍频率的采样系统；其次，要保证两倍关系的采样频率。

采样定理所描述的是一种理想采样情况下的数字控制系统与模拟控制系统之间的等价性，而对于任何实际系统应用采样定理时，都要进行适当地近似处理。第一，任何实际系统的频率成分都是十分复杂的，且一般都是无限带宽的。因此，要实现等价的数字控制系统就必须对原系统进行适当的滤波，除去与控制目标或者应用目标无关的高频成分，以滤波后的最高频率为系统的截止频率，并以此频率为基准确定采样频率，从而使得采样后的数字控制系统能够较为准确地反映原系统的特征。第二，采样定理所说采样信号是理想采样，即在采样点的采样数据与原系统完全相等。但对于实际采样系统，采样值本身也不可能与原系统的真实值完全相等，它也是一定精度下的近似值。所以，实际应用的采样系统是原系统在一定精度下的等价系统。

2.采样周期T0的确定

一般的生产过程都具有较大的时间常数，而数字PID控制系统的采样周期则要小得多，所以数字控制器的参数整定，完全可以按照模拟控制器的各种参数整定方法进行分析和综合。但是，数字控制器与模拟控制器相比，即除了比例系数、积分时间和微分时间外，还有一重要的参数——采样周期T0。合理地选择采样周期T0，也是数字控制系统的关键问题之一。

1）影响采样周期T0的扰动频率

扰动频率愈高，采样频率也应提高，采样周期应缩短。

2）被控对象的动态性

被控对象的动态性主要与被控对象的纯滞后时间τ及时间常数T有关。当纯滞后比较显著时，采样周期T0与τ/10基本相等。

3）控制的回路数

控制的回路越多，T0越大，否则T0越小。(www.daowen.com)

4）被控对象所要求的控制品质

一般来说，控制性能要求越高，采样周期越短，以减小系统的纯滞后。

采样周期的确定有2种方法：计算法和经验法。计算法由于比较复杂，特别是控制系统各环节时间常数难以确定，所以工程上用得比较少。工程上应用最多的还是经验法。

所谓经验法实际是试凑法，即根据人们在工作实践中积累的经验以及被控对象的特点、参数，先粗选一个采样周期T0，送入计算机控制系统进行试验，根据对被控对象的实际控制效果，反复改T0，直到满意为止。经验法所采用的采样周期，如表6-1所示。但在实际应用中，也需根据现场控制器型号、性能以及控制回路的多少，灵活调整采样周期的大小，特别是随着控制器性能提高，运算速度越来越快，采样周期的数值往往要提高一个数量级，进而提高控制系统的品质。

表6-1　采样周期的经验数据

在实际应用中还要注意执行器的动作时间，因为大部分执行器（如调节阀）在接收控制指令后要有一动作时间才能到位，因此片面地提高采样频率是没有意义的，一定要结合现场实际，经过综合考虑来确定采样周期。

3.模拟量的数字化

由于计算机只能处理数字量，因此数字控制系统必须将输入的模拟量转换成数字量。同时，数字控制器根据采样值和设定值完成相关计算后同样需要把数字量转换成模拟量输出到执行器。数字化流程如图6-3所示。

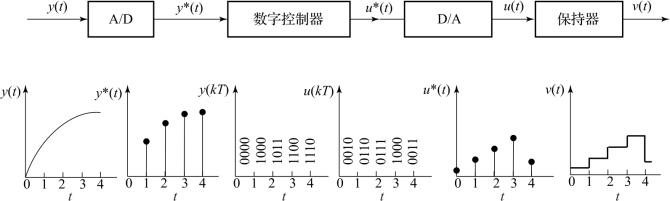
图6-3　数字化流程

4.数据采集

当模入点数不多时，可通过输入指令逐点读入；当模入点数较多时，可利用数据通道直接把一批数据送到内存指定的缓冲区，以节省时间。