1.PID控制器参数自整定的基本概念

传统的PID控制器参数是采用工程整定法且由人工整定，这种整定工作不仅需要熟练的技巧，往往还相当费时。更为重要的是，当被控对象特性发生变化需要控制器参数作相应调整时，传统的PID控制器没有这种“自适应”能力，只能依靠人工重新整定参数。由于生产过程的连续性及参数整定所需的时间，这种重新整定实际很难进行。如前所述，控制器的整定参数与系统控制品质是直接有关的，因此，多年来众多工程技术人员一直关注着控制器参数自整定的研究和开发。

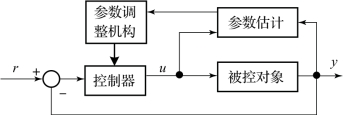
图5-15　自校正控制系统方框图

研究控制器参数自整定的目的是寻找一种对象验前知识不需要很多，既简单鲁棒性又好的方法。

图5-15所示的自校正控制器是调整控制器参数的一种方法。参数估计器首先假定被控对象为一阶线性模型，即

然后，利用控制变量u及被控变量y的测量值，应用工程整定法对被控对象参数K、T和τ值进行估计，一旦求出对象参数K、T和τ值，参数调整机构就能按照给定的整定规则（根据规定的闭环系统性能指标建立的对象参数与控制器参数的“最佳”值间的关系），求出控制器参数“最佳”值，修改控制器参数。

2.PID控制器参数自整定的方法

自校正控制器需要相当多的被控对象的验前知识，特别是需要知道有关对象时间常数的数量级，以便选择合适的采样周期或数字滤波器的时间常数。此外，参数估计器和调整机构均涉及大量计算，只有借助于数字计算机，该方法才能实现。这里仅讨论PID控制器的参数自整定。目前，基于继电器型反馈的极限环法是一种常用的PID控制器的参数自整定方法。它是瑞典学者Áström于1984年首先提出的，以下就这种方法进行详细讨论。

临界频率，即开环系统相角滞后180°时的频率，是整定PID控制器的关键参数。在PID控制器参数的稳定边界法的整定规则（见表5-3）中，这一频率是这样确定的，首先PID控制器置成纯比例作用，然后增大PID控制器比例增益，直到闭环系统处于稳定边界，此时系统的振荡频率即为临界频率ωcr（ωcr＝2π／T cr），这种实验有时很容易做，但是对于具有显著扰动的慢过程，这样的实验既费时又困难。为此，可以利用引入非线性因素使系统出现极限环，从而获得ωcr。基于极限环法具有继电器型反馈的自动整定器原理，如图5-16所示。使用整定器时，先通过人工控制使系统进入稳定工况，然后按下整定按钮，开关S接通B，获得极限环，最后根据极限环的幅值和振荡周期T cr计算出控制器参数值，继而控制器自动切至PID控制。

为防止由于噪声产生颤动，继电器应有滞环，同时反馈系统应使极限环振荡保持在规定的范围内。临界频率由系统输出过零的时间确定，而临界增益K cr（1/δcr）则由振荡的峰值确定。比较各个相隔半周期的输出测量值，就可以确认系统是否已获得稳定的不衰减振荡。这也是防止负荷扰动，判别系统进入稳定边界的简单的方法。极限环法必须提供的唯一的验前知识就是继电器特性幅值d的初始值，继电器滞环的宽度h由测量噪声级来确定。这种整定方法也可能因负荷扰动太大，不存在稳定的极限环，导致整定失败。

利用非线性元件的描述函数不难说明图5-17所示的控制系统具有继电器型非线性系统存在极限环的条件，以及确定振动的振幅和频率ωcr。

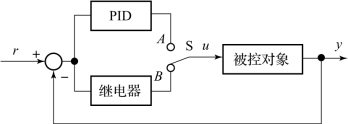
图5-16　继电器自动整定器原理框图(www.daowen.com)

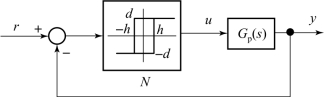
图5-17　具有继电器型非线性的控制系统框图

图中G p（s）为广义被控对象的传递函数，N表示非线性元件的描述函数，对于继电器型非线性，有

对于具有滞环的继电器非线性，有

式中：d为继电器型非线性特性的幅值；h为滞环的宽度；α为继电器非线性环节输入的一次谐波振幅。

只要满足方程

则系统输出将出现极限环。

在自整定过程中，闭环时系统输出和操作变量的振荡曲线如图5-18所示，其中操作变量u的信号幅值d＝0.05。临界振荡周期T cr如前所述，通过直接测量相邻两个输出过零的时间值确定。

极限环法的优点是，概念清楚，方法简单。但是，系统极限环是通过比较输出采样值加以判别的，而高频噪声等扰动会给采样值测量带来误差，这些都影响K cr、T cr值的精度。虽然存在以上不足，但极限环法仍不失为一种较好的控制器参数初步整定方法。需要注意的是，这种方法不是自适应的连续整定方法，而是由操作者根据控制特性状况间断进行的。

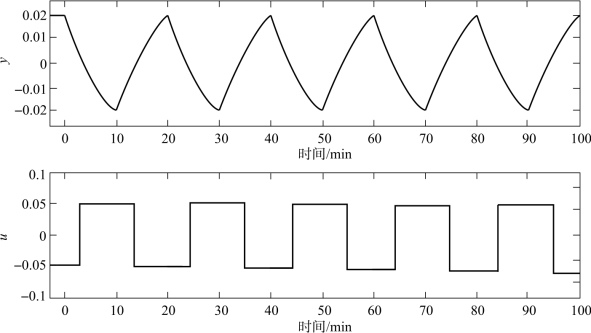
图5-18　自整定模式下系统输出和操作变量的振荡曲线