1.等效控制器

在利用动态特性参数法整定计算PID控制器参数时，需要把简单控制系统简化为等效控制器和广义被控对象两大部分。例如，将被控对象、执行器和检测变送装置合并为广义被控对象G p（s），而其他部分（包括比较机构）就是实际控制器。然而，在实际应用中，由于测试对象特性时，施加输入信号的位置不同，导致被控对象所包含的环节也不同，因此在定义广义被控对象时，也可以有不同的组合。广义被控对象可能仅包含被控对象和执行器或被控对象和检测变送仪表两部分，也可能只包含被控对象本身，这里将其称为等效广义被控对象，在不引起混淆的情况下，以下仍简称为广义被控对象，用G p（s）表示；另一部分（包括实际控制器）所包含的内容也可能不同，这里将其称为等效控制器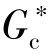（s），这时系统可以看成是由等效控制器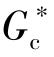（s）和广义被控对象Gp（s）组成，如图5-11所示。

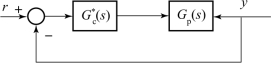
图5-11　由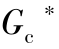（s）和G p（s）组成的简单控制系统框图

由于利用动态特性参数法整定计算所得的参数均为等效控制器的参数，所以必须经过换算后才能得到实际控制器（在不引起混淆的情况下，简称为控制器）的参数，等效控制器和广义被控对象之间如何划分直接影响实际控制器参数与等效控制器参数之间的关系，下面对其进行讨论。

（1）在通过试验测取动态特性时，如果调节阀并未考虑在广义被控对象的范围之内，则广义被控对象的传递函数G p（s）为

此时，等效控制器的传递函数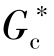（s）为

由于调节阀G v（s）可近似视为比例环节，即G v（s）＝K v。因此，当控制器为PID作用时，等效控制器的传递函数为

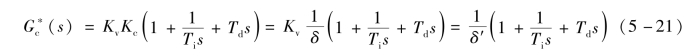
式中：δ为实际控制器的比例带；δ′＝1/（K v K c）为等效控制器的比例带；K v为调节阀的增益。

（2）如果试验测取的广义被控对象的动态特性已包括调节阀，即

则等效控制器就是实际控制器本身，即

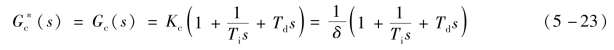
（3）如果用机理法求得被控对象的动态特性为G o（s），此时可认为广义被控对象G p（s）＝G o（s）。如将检测变送装置也近似视为比例环节，即G m（s）＝K m，那么当控制器为PID作用时，等效控制器的传递函数为

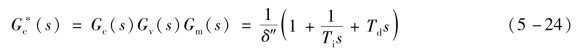
式中：δ″＝1/（K c K v K m）为等效控制器的比例带；K m为检测变送装置的转换系数；其余参数定义同上。

由上可知，实际控制器G c（s）等效控制器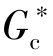（s）的参数中仅比例带不同，需进行转换。而其他两个参数积分时间T i和微分时间T d完全相同，不需转换。2.PID控制器参数的实际值与刻度值

根据以上方法整定计算得到的是实际工业PID控制器各参数的实际值。对于模拟PID控制器或早期仿模拟的数字PID控制器，由于采用阻容元件实现PID电路搭建，使得δ、T i和T d各参数之间存在相互扰动，必须考虑控制器各参数实际值与刻度值之间的转换关系。

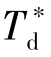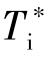由PID控制器动态特性分析可知，扰动系数式中：和分别为PID控制器微分时间和积分时间的刻度值；α为与PID控制器结构有关的系数。

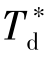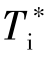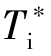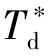对于不同类型的PID控制器，系数α各不相同，且随、取值不同而变化，通过分析可知，PID控制器整定参数的刻度值、实际值与扰动系数F之间的关系为式中：δ*、和分别为PID控制器比例带、积分时间、微分时间的刻度值；δ、T i和T d 分别为PID控制器比例带、积分时间、微分时间的实际值；F为扰动系数。

当PID控制器处于P、PI和PID工作状态时，F≈1；可近似地认为PD控制器参数的刻度值和实际值是一致的；当处于PID工作状态时，F＞1，且为的函数。所以，在整定PID控制器各参数时，必须按式（5-26）进行转换，由它的实际值计算PID控制器参数的刻度值，然后根据PD控制器参数的刻度值，对PID控制器进行设置。

【例5-1】对于如图5-12所示的温度控制系统，控制器采用PID调节规律。温度变送器量程为0～100℃，且温度变送器和PID控制器均为DDZ-III型仪表，系统在调节阀扰动量μ＝20%时，测得温度控制通道阶跃响应特性参数：稳定时温度变化Δθ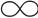（）＝60℃；时间常数T＝300 s；纯迟延时间τ＝10 s。试求PID控制器δ、T i和T d的刻度值（扰动系数F≈1）。

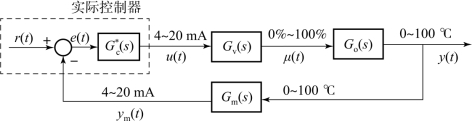
图5-12　温度控制系统方框图

解：（1）确定控制器的比例带。

由题可知，被控对象的传递函数为

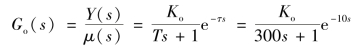
式中：。

如果检测变送装置和调节阀均近似视为比例环节，则根据图5-12可得检测变送装置的转换系数和调节阀的增益分别为

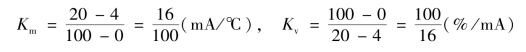
①如果广义被控对象的传递函数为

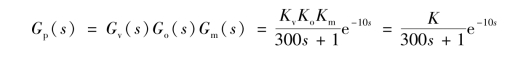
则广义被控对象的有关参数为：T＝300 s；τ＝10 s；K＝K o K v K m＝3。

采用动态特性参数法，按Z-N公式，有

计算等效控制器的等效比例增益，即

因为等效控制器仅由实际控制器本身组成，因此上式就是控制器比例增益的实际值，即K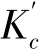＝。相应的比例带为

②如果广义被控对象不包括调节阀，即

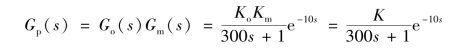(www.daowen.com)

则广义被控对象的有关参数为：T＝300 s；τ＝10 s；K＝K o K m＝3×16/100（mA/%）

采用动态特性参数法中按Z-N公式，有

计算等效控制器的等效比例增益，即

因为等效控制器由实际控制器和调节阀组成，因此

所以，控制器比例增益的实际值为

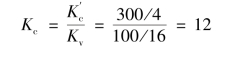
相应的比例带为

③如广义被控对象仅为被控对象本身，即

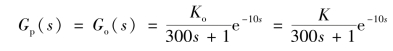
则广义被控对象的有关参数为：T＝300 s；τ＝10 s；K＝K o＝3（℃/%）。

采用动态特性参数法，按Z-N公式，有

计算等效控制器的等效比例增益，即

因为等效控制器由控制器、调节阀和检测变送装置组成，因此

所以控制器比例增益的实际值为

相应的比例带为

（2）确定控制器的积分时间和微分时间。

由公式T i＝2.0τ，得控制器积分时间的实际值

由公式T d＝0.5τ，得控制器微分时间的实际值

（3）确定控制器比例带和积分时间的刻度值。

因为PID控制器的扰动系数F＝1，故控制器参数的实际值就是它的刻度值。

由上例可知，进行PID参数整定时，不论广义被控对象如何划分，其计算结果是一样的。

【例5-2】广义被控对象G p（s）的传递函数为

已知时间单位为s，试利用Z-N公式整定方法，计算系统采用P、PI、PID调节规律的PID控制器参数，并绘制整定后系统的单位阶跃响应曲线。

解：由广义被控对象的传递函数可知：K＝1，T＝360 s，τ＝180 s。根据Z-N整定公式可得

（1）P控制时：K c＝0.25；

（2）PI控制时：K c＝0.225，T i＝599 s；

（3）PID控制时：K c＝0.30，T i＝360 s，T d＝90 s。

利用图5-13所示的Simulink系统仿真图，分别在Switch K1、Switch K2断开，Switch K1闭合、Switch K2断开和Switch K1、Switch K2全闭合3种情况下得到如图5-14所示的系统在P、PI、PID控制时的单位阶跃响应曲线。图中的参数K c、T i、T d根据控制规律不同分别设置不同的整定参数。

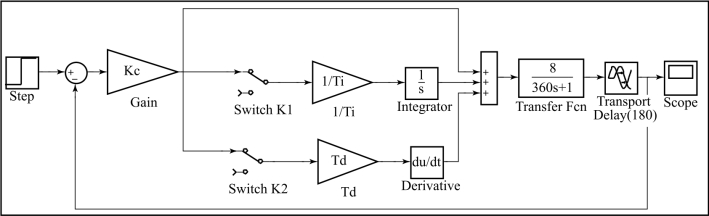
图5-13　Simulink系统仿真图

由仿真结果可见，采用纯P控制时，系统是有差调节，调节速度较快；采用PI控制时，可以实现系统无差调节，但调节时间变长；采用PID控制时，系统即实现无差调节，同时与PI控制相比，系统工作频率高、超调量小，调节时间短，这也说明了当0.2≤τ／T≤1时，采用PID控制有更好的控制效果。

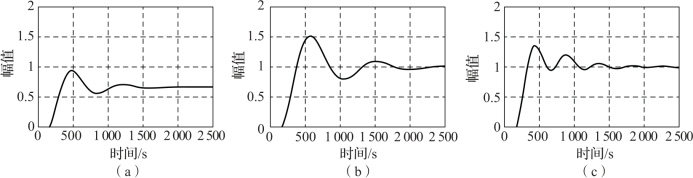
图5-14　系统单位阶跃响应曲线（Z-N整定法）

（a）P控制；（b）PI控制；（c）PID控制