衰减曲线法与稳定边界法类似，区别在于衰减曲线法通过某衰减比（通常为4∶1或10∶1）时设定值扰动的衰减振荡试验数据，采用一些经验公式求取PID控制器相应的整定参数。对于4∶1衰减曲线法的具体步骤如下。

（1）置控制器积分时间T i为最大值（T i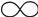＝），微分时间T d为0（T d＝0），比例带δ置较大值，并将系统投入运行。

（2）待系统稳定后，作设定值阶跃扰动，并观察系统的响应。若系统响应衰减太快，则减小比例带；反之，系统响应衰减过慢，应增大比例带。如此反复，直到系统出现如图5-10（a）所示的4∶1衰减振荡过程，记下此时的比例带δs和振荡周期T s数值。

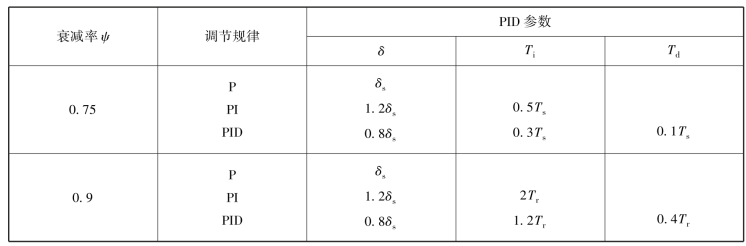
（3）用δs和T s值，按表5-5给出的经验公式，求控制器整定参数δ、T i和T d的数值。

对于扰动频繁，过程进行较快的控制系统，要准确地确定系统响应的衰减程度比较困难，往往只能根据控制器输出摆动次数加以判断。对于4∶1衰减过程，控制器输出应来回摆动两次后稳定。摆动一次所需时间即为T s。显然，这样测得的T s和δs值，会给控制器参数整定带来误差。

衰减曲线法也可以根据实际需要，在衰减比为n＝10∶1的情况下进行。此时，要以图5-10（b）中的上升时间T r为准，按表5-5给出的公式计算。(www.daowen.com)

以上介绍的几种系统参数工程整定法有各自的优缺点和适用范围，要善于针对具体系统的特点和生产要求，选择适当的整定方法。不管用哪种方法，所得PID控制器整定参数都需要通过现场试验，反复调整，直到取得满意的效果为止。

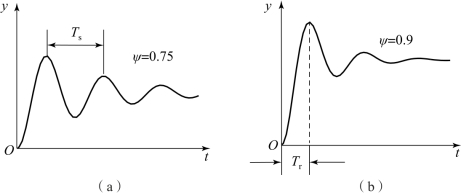
图5-10　系统衰减响应

表5-5　衰减曲线法整定计算公式