动态特性参数法是以被控对象控制通道的阶跃响应曲线为依据，通过一些经验公式求取控制器最佳参数整定值的开环整定方法。

用动态特性参数法计算PID控制器参数整定值的前提是，将系统简化为由控制器G c（s）和广义被控对象G p（s）组成。其中，广义被控对象的阶跃响应曲线可用一阶惯性环节加纯迟延来近似，即

否则根据以下几种动态特性参数整定方法得到的

中的PID控制器中整定参数只能作初步估计值。

1.Z-N工程整定法

Z-N工程整定法是由齐格勒（Ziegler）和尼科尔斯（Nichols）于1942年首先提出的，计算PID控制器参数的公式见表5-1。

表5-1　Z-N控制器参数整定公式

注：上述整定规则仅限于0＜τ＜T。

2.C-C工程整定法

在Z-N工程整定法的基础上，经过不断改进，总结出相应的计算PID控制器最佳参数整定公式。这些公式均以衰减率（ψ＝0.75）为系统的性能指标，其中广为流行的是柯恩（Cohen）　-库恩（Coon）整定公式，即

（1）比例控制器

（2）比例积分控制器

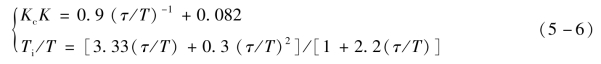(www.daowen.com)

（3）比例积分微分控制器

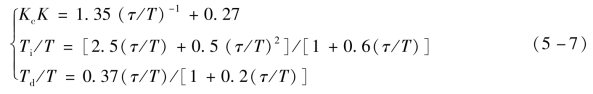
3.Lambda整定法

Lambda整定是一种内模控制（IMC）的形式，它能够使比例积分（PI）控制器在设定点变化时实现平滑、不振荡的控制效果。它的名字来自希腊字母λ（lambda），这是一个影响响应过程的参数，表示控制器将过程变量从起点移动到设定值需要花费多少时间。计算PID参数的公式见表5-2。

表5-2　Lambda控制器参数整定公式

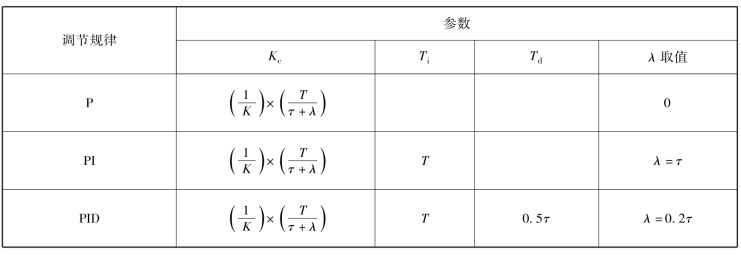
注：上述整定规则不受τ／T的限制。

从表5-2可见，只要已知对象的K、T、τ，并指定性能参数λ的值，就可以根据表中公式计算PID参数。需要注意的是，Lambda整定适合于响应过程不要求很快且不希望有超调振荡的场合。这也是Lambda整定在造纸作业中应用比较普及的原因，因为某些过程变量的振荡会给最终产品带来视觉可见的瑕疵。

4.以各种误差积分值作为系统性能指标的工程整定方法

随着计算机控制系统的广泛应用，又提出了以各种误差积分值作为系统性能指标的PID控制器最佳参数整定公式，即

整定公式中的各系数在不同误差积分性能指标下的取值见表5-3。

表5-3　Z-N及IAE、ISE、ITAE性能指标的各系数取值

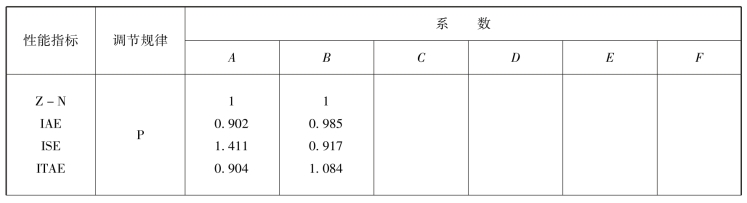
续表

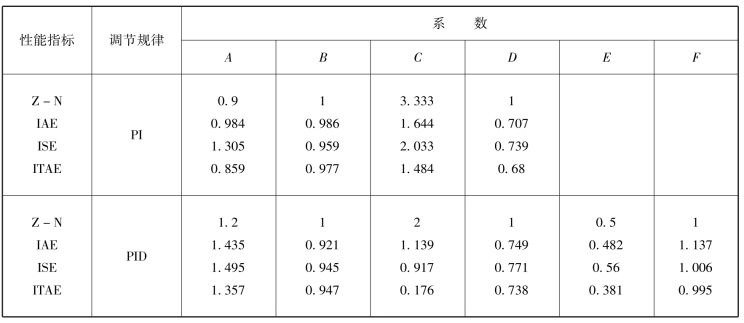
注：为便于比较，表中也列入了Z-N整定方法计算公式。