在稳态情况下，d e/d t＝0，PD控制的微分部分输出为零，因此PD控制也是有差调节。式（4-16）表明，微分控制总是力图抑制被控变量的振荡，提高控制系统稳定性的作用。适度引入微分动作较纯比例控制可以允许稍微减小比例带，同时保持衰减率不变。图4-15表示同一被控对象分别采用P控制器和PD控制器并整定到相同的衰减率时，两者控制效果的比较。从图中可以看到，适度引入微分动作后，由于PD可以采用较小的比例带，结果不但减小了余差，而且也减小了短期最大偏差并提高了振荡频率。

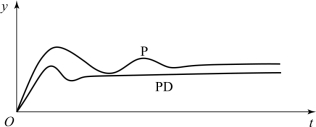
图4-15　P控制与PD控制效果比较

以上的结论也可以很容易地根据控制理论加以验证。因微分的引入，将在s左半平面引入一个开环0点，根轨迹向有利于提高系统稳定性的方向移动。这说明，对同一被控对象，PD控制的稳定性要高于P控制，即微分的引入改善了系统的稳定性。

微分控制动作也有一些不利之处。首先，微分动作太强容易导致调节阀开度向两端饱和；其次，微分会使消除误差的过程变缓，甚至形成“爬行”的响应曲线，因此在PD控制中总是以比例动作为主，微分动作只能起辅助控制作用；再次，PD控制器的抗扰动能力差，只能用于被控变量变化非常平稳的过程，一般不用于流量和液位控制系统；最后，微分控制动作对于纯迟延过程是无效的。应当特别指出，引入微分动作要适度。这是因为虽然大多数PD控制系统随着微分时间T d增大，其稳定性提高，但也有例外，某些特殊系统的T d超出某一上限值后，系统反而变得不稳定了。图4-16为控制系统在不同微分时间的响应过程。

图4-16　PD控制在不同T d的响应过程

（a）T d太小；（b）T d适当；（c）T d太小；（d）T d＝0(www.daowen.com)

【例4-6】已知系统方框图如图4-4所示。其中，控制器G c（s）和广义被控对象G p（s）的传递函数分别为

试利用MATLAB绘制比例增益K c＝2，微分时间T d＝0，1，2，3，5，7时，系统在单位阶跃输入信号作用下的输出响应。

解：利用如下的MATLAB程序，可得如图4-17所示的阶跃响应曲线。

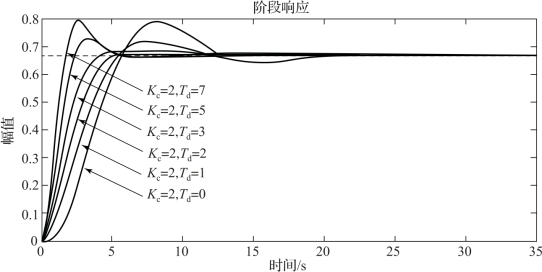
图4-17　比例微分控制单位阶跃输入响应曲线

由图4-17可知，在采用PD控制时，系统的稳态误差不为0。系统适度引入微分后，随着微分时间增大，超调量减小，上升时间减小，快速性提高。当微分时间T d超过某一值后，系统的稳定性反而会随着T d变大而下降。