积分控制虽然可以做到消除稳态误差，但积分控制的输出同误差的累计相关，而不是与误差当前的大小相关。误差产生的初期，误差数值较小，调节作用弱，调节相对滞后，所以积分控制一般不单独使用，通常与比例控制联合使用，构成比例积分控制。

比例积分控制（PI控制）就是综合比例和积分两种控制的优点，利用比例控制快速抵消扰动的影响，同时利用积分控制消除余差，其控制规律为

或

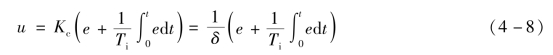
式中：K c称为比例增益；K i称为积分增益；δ为比例带，可视情况取正值或负值；T i为积分时间。其中，δ和T i是PI控制器的2个重要参数。

PI控制器的传递函数为

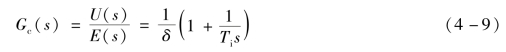
图4-8是PI控制器的阶跃响应，由比例动作和积分动作组成。

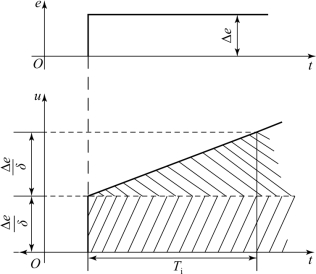
图4-8　PI控制器的阶跃响应

在施加阶跃输入的瞬间，控制器立即输出一幅值为Δe／δ的阶跃，然后以固定速度Δe／（δT i）变化。当t＝T i时，控制器的总输出为2Δe／δ。这样，就可以根据式（4-7）确定δ和T i的数值。另外，当t＝T i时，输出的积分部分正好等于比例部分。由此可见，T i可以衡量积分部分在总输出中所占的比重，T i越小，积分部分所占的比重越大。积分越大（K i增加或T i减小），消除稳态误差越快；积分越小（K i减小或T i增加），消除稳态误差越慢。

应当指出，PI控制引入积分动作带来消除系统余差好处的同时，却降低了原有系统的稳定性。为保持控制系统与比例控制具有相同的衰减率，PI控制器的比例带较纯比例控制应适当加大。所以，PI控制是在稍微牺牲控制系统的动态品质的情况下来换取系统无稳态误差的。(www.daowen.com)

PI控制中，在比例带不变的情况下，减小积分时间T i，将使控制系统稳定性降低、振荡加剧，直到最后出现发散的振荡过程。图4-9为PI控制系统不同积分时间的响应过程。

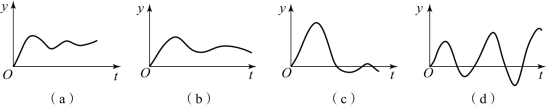
图4-9　PI控制系统不同积分时间的响应过程

（a）T i无限大；（b）T i太大；（c）T i适当；（d）T i太小

【例4-5】已知系统方框图如图4-4所示。其中，控制器G c（s）和广义被控对象G p（s）的传递函数分别为

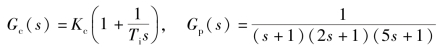
试利用MATLAB绘制比例增益K c＝2，积分时间T i＝5，6，8，11，15，20时，系统在单位阶跃输入信号作用下的输出响应。

解：利用如下的MATLAB程序，可得如图4-10所示的阶跃响应曲线。

图4-10　比例积分控制单位阶跃输入响应曲线

由图4-10可知，采用PI控制时，系统的稳态误差总是为0（参数在一定范围内），但在比例增益不变，积分时间变小时，系统的稳定性降低，振荡加剧，振荡频率升高。