4.2节的分析表明，比例控制无法做到稳态误差为0，这就无法满足一些要求较高的控制系统。分析原因，发现比例控制是将当前存在的误差放大K c倍，进而驱动执行机构，用于消除误差。换句话说，误差的当前值是消除误差的基础。误差越小，控制器的输出也越小，因此这种方式无法彻底消除误差。那能否让误差很小时甚至为0时控制器还有足够的输出呢？积分环节的特点正好可以满足这一要求。积分控制的输出不仅与误差的大小相关，还与误差的累计相关，只要误差不为0，积分环节输出将持续变化，误差等于0时，积分环节输出保持不变。

1.积分控制的输入输出关系

在积分控制（或I控制）中，控制器的输出信号的变化速度d u／d t与偏差信号e成正比，即

式中：K i称为积分增益。

式（4-6）表明，控制器的输出与偏差信号的积分成正比。

2.积分控制的特点

积分控制的特点是无差制。积分调节可以做到稳态无差的原因在于积分作用输出与误差的累计相关，而不是与误差当前的大小相关。式（4-6）表明，只有当被控变量偏差信号e为0时，积分控制器的输出才会保持不变。与此同时，控制器的输出却可以停在任何数值上。这意味着被控对象在负荷扰动下的控制过程结束后，被控变量没有余差，而调节阀则可以停在新的负荷所要求的开度上。采用积分控制的控制系统，其调节阀开度与当时被控变量的数值本身没有直接关系。因此，积分控制也称为浮动控制。

【例4-4】已知系统方框图如图4-4所示，试分析系统在阶跃给定信号作用下的稳态特性。其中，控制器G c（s）和广义被控对象G p（s）的传递函数分别为(www.daowen.com)

解：系统在幅值为A的阶跃给定信号r（t）＝A·1（t）作用下的稳态误差为

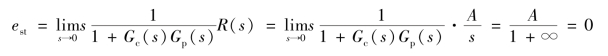
由此可知，该系统采用积分控制时，在阶跃给定信号作用下的稳态误差始终为0。

积分控制的另一特点是它的稳定作用比比例控制差。例如，根据奈氏稳定判据可知，对于非自衡的被控对象采用比例控制时，只要加大比例带总可以使系统稳定（除非被控对象含有一个以上的积分环节）；如果采用积分控制则不可能得到稳定的系统。

对于同一被控对象若分别采用比例控制和积分控制，并调整到相同的衰减率（ψ＝0.75），则它们在负荷扰动下的控制过程如图4-7中曲线P和曲线I所示。它们清楚地显示出2种控制规律的不同特点。

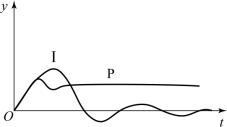
图4-7　比例控制和积分过程