比例控制的特点就是有差控制，即将当前存在的误差放大K c倍，进而驱动执行机构，用于消除误差。换句话说，比例控制中误差的当前值是消除误差的基础。误差越小，控制器的输出也越小，因此这种方式无法彻底消除误差。

工业过程在运行中经常会发生负荷变化，所谓负荷是指物料流或能量流的大小。处于自动控制下的被控对象在进入稳态后，流入量与流出量之间总是达到平衡的。因此，人们常常根据调节阀的开度来衡量负荷的大小。如果采用比例控制，则在负荷扰动下的控制过程结束后，被控变量不可能与设定值准确相等，之间一定有余差，即系统存在稳态误差。

图4-2为一热水加热器的出口水温控制系统。在这个控制系统中，热水温度θ是由温度测量变送器θT获取信号并送到温度控制器θC，控制器控制加热蒸汽的调节阀开度。

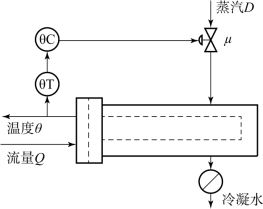
图4-2　加热器的出口水温控制系统

调节阀开度μ用以保持出口水温恒定，加热器的热负荷既取决于热水流量Q也取决于热水温度θ的值。假定现在采用比例控制器，并将μ直接视为控制器的输出。

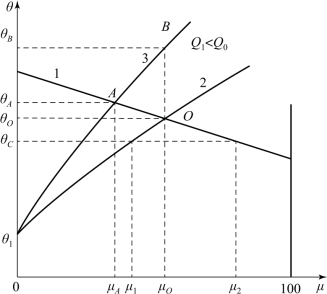
图4-3　比例控制器的静特性

图4-3中的直线1是比例控制器的静特性，即调节阀开度随水温变化的情况。水温越高，控制器应把调节阀开得越小，因此它在图中是左高右低的直线，比例带越大，则直线的斜率越大。图中曲线2和曲线3分别是加热器在不同的热水流量下的静特性，它们表示没有控制器控制时，加热器在不同的热水流量下的稳态出口水温与调节阀开度之间的关系，可以通过单独对加热器进行的一系列实验得到。直线1与曲线2的交点O代表在热水流量为Q0业已投入自动控制并假定控制系统是稳定的情况下，最终要达到的稳态运行点，那时的出口水温为θO，调节阀开度为μO。如果假定就是水温θO的设定值（这可以通过调整控制器的工作点做到），从这个运行点开始，如果热水流量减小为Q1，那么在控制过程结束后，新的稳态运行点将移到直线1与曲线3的交点A。这就出现了被控变量余差θA-θO，它是比例控制规律所决定的。不难看出，余差既随着流量变化幅度变化，也随着比例带的加大而加大。比例控制虽然不能准确保持被控变量恒定，但效果还是比不加自动控制好。在图4-3中，从运行点O开始，如果不进行自动控制，那么热水流量减小为Q1后，水温将根据其自平衡特性一直上升到θB为止。

从热量平衡观点看，在加热器中，蒸汽带入的热量是流入量，热水带走的热量是流出量。在稳态下，流出量与流入量保持平衡。无论是热水流量还是热水温度的改变，都意味着流出量的改变，此时必须相应地改变流入量才能重建平衡关系。因此，蒸汽调节阀开度必须有相应的改变。从比例控制器看，这就要求水温必须有余差。下面通过一例子从理论上对以上的结论进行验证。

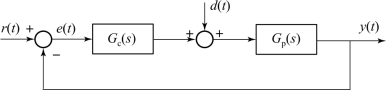
【例4-1】已知系统方框图如图4-4所示，试分析系统在阶跃给定信号作用下的稳态特性。其中，控制器G c（s）和广义被控对象G p（s）的传递函数分别为

(www.daowen.com)

解：系统在幅值为A的阶跃给定信号r（t）＝A·1（t）作用下的稳态误差为

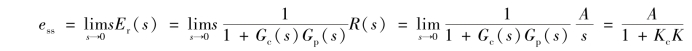
由此可见，该系统采用比例控制时，在阶跃给定信号作用下的稳态误差与输入的幅值成正比，与其开环增益K c K成反比，且是一个有限值。也就是说，只要广义被控对象的增益K c与控制器的增益K的乘积不为无穷大，系统的稳态误差就不会为0。

加热器的控制是具有自衡特性的工业过程，另有一类过程则不具有自衡特性，工业锅炉的水位控制就是一个典型例子。这种非自衡过程本身没有所谓的静特性，但仍可以根据流入、流出量的平衡关系进行有无余差的分析。为了保持水位稳定，给水量必须与蒸汽负荷取得平衡，一旦失去平衡关系，水位就会一直变化下去。因此，当蒸汽负荷改变后，在新的稳态下，给水调节阀开度必须有相应的改变，才能保持水位稳定。如果采用比例控制器，当蒸汽负荷改变后，这就意味着水位必须有余差。但水位设定值的改变不会影响锅炉的蒸汽负荷，因此在水位设定值改变后，水位不会有余差。

下面通过一例子从理论上对以上的结论进行验证。

【例4-2】已知系统方框图如图4-4所示，试分析系统在阶跃信号作用下的稳态特性。其中，控制器G c（s）和广义被控对象G p（s）的传递函数分别为

解：（1）系统在幅值为A的阶跃给定信号r（t）＝A·1（t）作用下的稳态误差为

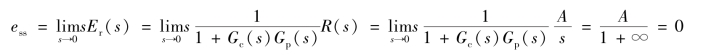
（2）系统在幅值为A的阶跃扰动信号d（t）＝A·1（t）作用下，且G c（s）G p（s）≫1时，其稳态误差为

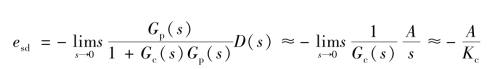
由此可见，无自衡特性的对象采用比例控制时，系统在阶跃给定信号作用下的稳态误差为0，但在阶跃扰动信号作用下的稳态误差不会为0。