以上讨论的是只有一个储能元件的对象,实际被控对象往往要复杂一些,即具有一个以上的储能元件。
1.串联型双容水槽
对于图2-8所示的双容水槽。水首先进入水槽1,然后通过底部的负载阀R1流入水槽2。水流入量Q i由进入水槽1的调节阀开度μ加以控制,流出量Q o由用户根据需要通过负载阀R2来改变,被控变量为水槽2的液位H2。现在分析水槽2的液位H2在调节阀开度μ扰动下的动态特性。
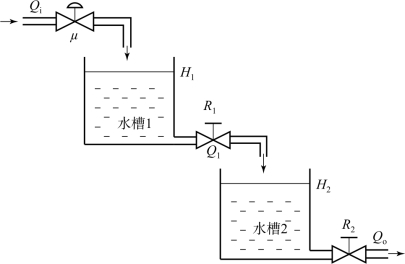
图2-8 串联型双容水槽
根据图2-8可知,水槽1和水槽2的物料平衡方程分别为
水槽1

水槽2

假设调节阀均采用线性阀,则有
![]()
式中:F1、F2分别为水槽1和水槽2的横截面积;R1和R2为负载阀的线性化水阻。
将式(2-24)代入式(2-22)和式(2-23)中,消去中间变量后可得
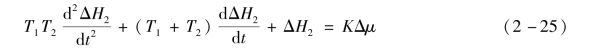
式中:T1=R1 F1;T2=R2 F2;K=kμR2。
对应式(2-25)的传递函数为
![]()
由式(2-26)可知,双容水槽为二阶系统,其阶跃响应曲线如图2-9所示。由图可知,双容水槽的阶跃响应曲线不是指数曲线,而是呈“S”形,它在起始阶段与单容水槽的阶跃响应曲线有很大的差别。对于双容水槽,在调节阀突然开大后的瞬间,液位H1只有一定的变化速度,而其变化量本身为0,因此Q1暂无变化,这时H2的起始变化速度为0。每增加一个容积对象,会使得阶跃响应曲线相应向后推迟,推迟的时间称为容量迟延,图2-11(b)中用τq表示。
若双容水槽存在纯迟延τ0,容量迟延τq,则总的迟延时间τ=τ0+τq,对应的传递函数为
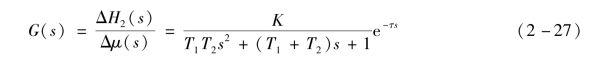
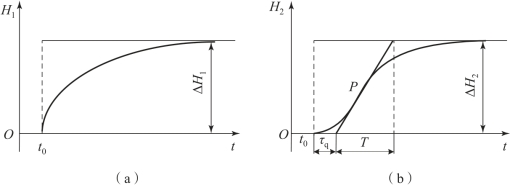
图2-9 双容水槽的阶跃响应曲线
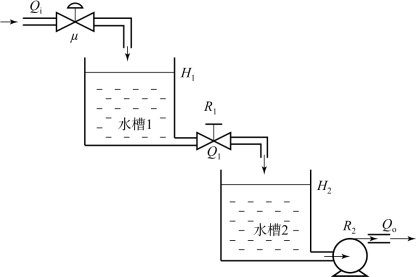
2.串联型双容积分水槽
串联型双容积分水槽无自平衡能力,如图2-10所示,它与图2-8所示的有自平衡能力的双容水槽只有一个区别,即在水槽2的流出侧装有一个排水泵,并取消了负载阀。此水槽1和水槽2的物料平衡方程分别为
水槽1

水槽2

 (www.daowen.com)
(www.daowen.com)
图2-10 串联型双容积分水槽
假设调节阀均采用线性阀,则有
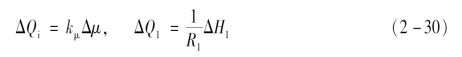
式中:F1和F2分别为水槽1和水槽2的横截面积;kμ为调节阀的线性化系数;R1为负载阀的线性化水阻。
将式(2-30)代入式(2-28)和式(2-29)中,整理后可得
![]()
对应式(2-31)的传递函数为
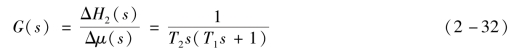
式中:T1=R1 F1;T2=F2/kμ。
式(2-32)对应的阶跃响应曲线如图2-11所示。
3.并联型双容水槽
对于图2-12所示的双容水槽,2个水槽串联在一起,每个水槽的液位变化都会影响另一个水槽的液位。另外,由于水槽之间的连通管路具有一定的阻力,因此两者的液位可能是不同的。水首先进入水槽1,然后通过连通管进入水槽2,最后由水槽2流出。水流入量Q i由进入水槽1的调节阀开度μ加以控制,流出量Q o由用户根据需要通过负载阀R2来改变,被控变量为水槽2的液位H2。下面分析水槽2的液位H2在调节阀开度μ扰动下的动态特性。
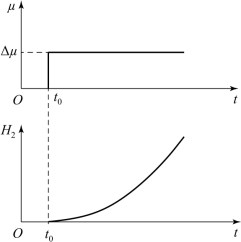
图2-11 串联型双容积分水槽的阶跃响应曲线
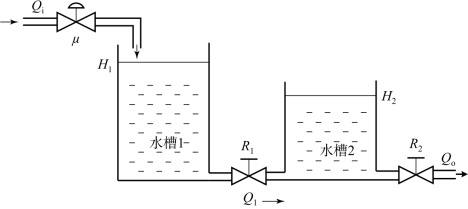
图2-12 并联型双容水槽
根据图2-12可知,水槽1和水槽2的物料平衡方程分别为
水槽1
![]()
水槽2
![]()
假设调节阀均采用线性阀,则有
![]()
式中:F1和F2分别为水槽1和水槽2的横截面积;kμ为调节阀的线性化系数;R1和R2为负载阀的线性化水阻。
将式(2-35)代入式(2-33)和式(2-34)中,整理后可得式
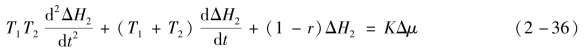
式中: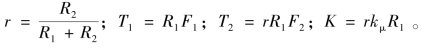
对应式(2-36)的传递函数为
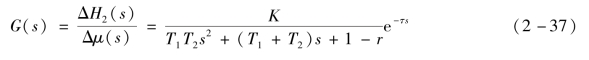
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








